Согласно Холланду генетические схемы поиска оптимальных решений включают следующие этапы процесса эволюции:
1. Конструируется начальная популяция. Вводится начальная точка отсчета поколений t = 0. Вычисляются приспособленность хромосом популяции (целевая функция) и средняя приспособленность всей популяции.
2. Устанавливается значение t = t+1. Выбираются два родителя (хромосомы) для кроссинговера. Выбор осуществляется случайным образом пропорционально жизнеспособности хромосом, которая характеризуется значениями целевой функции.
3. Формируется генотип потомка. Для этого с заданной вероятностью над генотипами выбранных хромосом производится операция кроссинговера. Случайным образом выбирается один из потомков A(t), к которому с заданными вероятностями последовательно применяются операторы инверсии и мутации. Полученная хромосома сохраняется как A’(t).
4. Обновление текущей популяции путем замены случайно выбранной хромосомы на A’(t).
5. Определение приспособленности A’(t) и пересчет средней приспособленности популяции.
6. Если t=t*, где t* – заданное число шагов, то переход к этапу 7, в противном случае – переход к этапу 2.
7. Конец работы.
Основная идея эволюции, заложенная в различные конструкции генетических алгоритмов, проявляется в способности «лучших» хромосом оказывать большее влияние на состав новой популяции за счет длительного выживания и более многочисленного потомства.
Простой генетический алгоритм включает операцию случайной генерации начальной популяции хромосом и ряд операторов, обеспечивающих генерацию новых популяций на основе начальной. Этими операторами являются репродукция, кроссинговер и мутация.
Репродукцией называется процесс копирования хромосом с учетом значений целевой функции, т.е. хромосомы с «лучшими» Значениями целевой функции имеют большую вероятность попадания в следующую популяцию. Этот процесс является аналогией митозного деления клеток. Выбор клеток (хромосом) для репродукции проводится в соответствии принципом «выживания сильнейшего». Простейшим способом представления операции репродукции в алгоритмической форме является колесо рулетки, в котором каждая хромосома имеет поле, пропорциональное значению целевой функции.
В алгоритмических реализациях механизма воспроизводства хромосом следует придерживаться следующих правил.
1. Выбор начальной популяции можно выполнять произвольным образом, например подбрасыванием монеты.
2. Репродукция осуществляется на основе моделирования движения колеса рулетки.
3. Оператор кроссинговера реализуется как взаимный обмен короткими фрагментами двоичных строк гомологичных хромосом.
4. Вероятность оператора кроссинговера принимается равной Р(CO)<1.
5. Вероятность оператора мутации принимается равной Р(МO)>0.001.
Рассмотрим пример применения простого генетического алгоритма для максимизации функции f(x)=x2 на целочисленном интервале [0, 31].
Значения аргумента функции изменяющегося в интервале от 0 до 31, можно представить пятиразрядными двоичными числами. Первоначальная популяция, состоящая из четырех пятиразрядных чисел, получена с помощью процедуры генерации случайных чисел.
Анализ начальной популяции на первом шаге простого генетического алгоритма:
| Номер хромосомы | Значение х (десятичный код) | Двоичный код хромосомы | Значение целевой функции | Вероятность выбора | Ожидаемое количество копий хромосомы в следующем поколении | Реальное количество копий хромосомы в следующем поколении |
| 0.14 0.49 0.06 0.31 | 0.56 1.96 0.24 1.24 | |||||
| Сумма | 1.00 | 4.00 | ||||
| Среднее значение | 0.25 | 1.00 | ||||
| Максимальное значение | 0.49 | 1.97 |
Вероятность выбора i-й хромосомы вычисляется по формуле
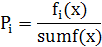
где fi(x) — значение целевой функции i-й хромосомы в популяции; sumf(x) – суммарное значение целевой функции всех хромосом в популяции.
Ожидаемое число копий i-й хромосомы после оператора репродукции равно
N = Pin;
где n — Число анализируемых хромосом.
Репродукция начального множества заключается в четырехкратном вращении колеса рулетки (4 - мощность популяции), в результате чего состав исходной популяции может измениться.
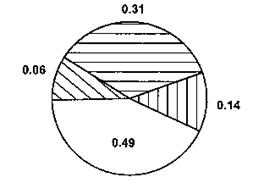
Рисунок 10.4 – Колесо рулетки.
Следует заметить, что колесо рулетки не гарантирует выбора лучших хромосом, т.е. иногда результатом выбора могут оказаться хромосомы с низкими значениями целевой функции.
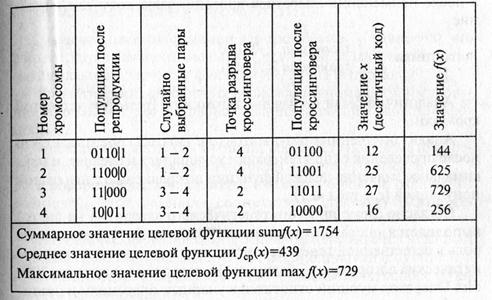
После репродукции выполняется оператор кроссинговера, который может повторяться несколько раз. При этом каждый раз будет осуществляться выбор двух кандидатур из множества хромосом. Затем каждая пара хромосом пересекается. Место пересечения К выбирается случайным образом на интервале (1, L-1), где L – длина хромосомы, определяемая количеством значащих цифр в ее двоичном коде. В нашем случае L = 5. Две новые хромосомы создаются путем взаимного обмена всех значений после точки пересечения, т.е. между позициями (К+1) и L. При выборе двух первых хромосом из популяции (см. табл) и значения К = 4 до применения оператора кроссинговера имеем описание:
хромосома1: 0110|1
хромосома2: 1100|0
После применения оператора кроссинговера получаем описание:
хромосома1: 0110|0
хромосома2: 1100|1
Аналогично были получены потомки от третьей и четвертой хромосом.
Анализ полученных результатов показывает, что после проведения одной генерации улучшились и среднее, и максимальное значение целевой функции по сравнению с начальной популяцией.
Согласно схеме простого генетического алгоритма на шаге 3 выполняется оператор мутации, который играет существенную роль в естественной генетике и эволюции, но менее значим в генетических алгоритмах. Обычно выбирают одну мутацию на 1000 бит. Оператор мутации относится к унарным операциям и реализуется в два этапа.
Этап 1. В хромосоме А = {а1, а2, a3…aL-2, aL-1, aL} случайным образом определяют две позиции, например, 2 и L-1.
Этап 2. Гены, соответствующие выбранным позициям, меняют местами и формируют новую хромосому А = {а1, aL-1, a3,…, aL-2, a2, aL}
Если длина обрабатываемых последовательностей невелика, то в процессе мутации можно осуществить полный перебор возможных перестановок генов и найти комбинацию с максимальным значением целевой функции. Выберем третью хромосому 11011 со значением целевой функции f(х)=729 и применим операцию мутации к позициям 3 и 4:
хромосома 3: 11011 -> хромосома 3': 11101.
У новой хромосомы 3' значение целевой функции равно (29)2=841. Сделаем еще одну перестановку 4 и 5 генов в хромосоме 3':
хромосома 3': 11101 –> хромосома 3": 11110.
Значение целевой функции для хромосомы 3" равно 900, что соответствует квазиоптимальному решению задачи нахождения максимального значения функции f(х)=x2 на интервале [0,31].
 2014-02-09
2014-02-09 1956
1956








