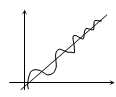
 Опр. Прямая наз-ся асимптотой кривой, если расстояние
Опр. Прямая наз-ся асимптотой кривой, если расстояние 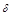 от переменной точки
от переменной точки 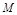 кривой при удалении точки
кривой при удалении точки 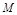 в
в 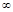 стремится к 0, т.е.
стремится к 0, т.е. 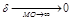 .
.
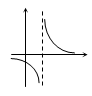 Опр. Прямая
Опр. Прямая 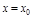 яв-ся вертикальной асимптотой графика ф-ции
яв-ся вертикальной асимптотой графика ф-ции 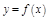 , если
, если 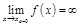 или
или 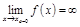 (т.е. т.
(т.е. т.  яв-ся точкой разрыва 2-го рода ф-ции
яв-ся точкой разрыва 2-го рода ф-ции 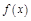 ).
).
ПР. 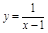
Пусть прямая 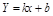 яв-ся наклонной асимптотой графика ф-ции
яв-ся наклонной асимптотой графика ф-ции 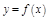 . Найдем
. Найдем 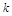 и
и 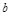 .
.

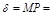
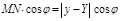 .
. 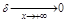 ,
, 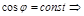
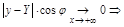
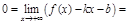
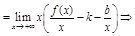
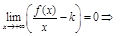
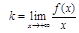 (1)
(1)
_______________________________________________________
Найдем 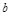 :
:
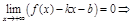
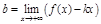 (2)
(2)
Если хотя бы один из пределов (1) или (2) не существует или бесконечен, то наклонной асимптоты при 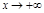 нет.
нет.
При 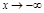 аналогично.
аналогично.
ПР. 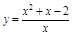 ;
;
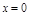 – верт. ас-та;
– верт. ас-та; 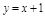 – накл. ас-та.
– накл. ас-та.
§ 4. Общая схема исследования ф-ции и построения графика.
1. Исследование вида зависимости 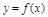 :
:
a) область определения;
b) точки разрыва;
c) четность и нечетность;
d) периодичность;
e) точки пересечения с осями координат;
2. Асимптоты:
a) вертикальные;
b) наклонные.
3. Исследование по первой производной:
a) критические точки 1-го порядка;
b) участки монотонности;
c) точки локальных экстремумов.
4. Исследование по второй производной:
a) критические точки 2-го порядка;
b) участки выпуклости и вогнутости;
c) точки перегиба.
5. Исследование поведения функции на концах области определения.
6. Построение графика с учетом результатов, полученных в пунктах 1-5.
Пр. 1) 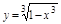
1.
a) 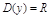
b) непрерывна
c) 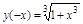 – ф-ция общего вида
– ф-ция общего вида
d) непериодическая
e) 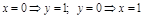
2.
a) ф-ция непрерывна Þ вертикальных асимптот нет
b) 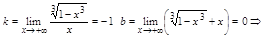
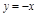
3. 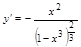
a) критические точки 1-го порядка: 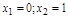
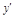 – – –
– – –
b) 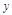 0 1 x
0 1 x
c) экстремумов нет
4. 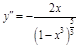
a) критические точки 2-го порядка: 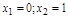

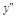 + – +
+ – +
b) 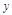
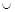 0
0 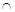 1
1  x
x
c) 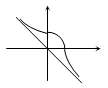 точки перегиба:
точки перегиба: 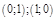
5.
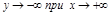 ,
, 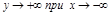
ПР. 2. 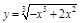 .
.
1.
a) 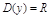
b) непрерывна
c) ф-ция общего вида
d) не периодическая
e) 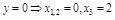
_______________________________________________________
2.
a) ф-ция непрерывна Þ вертикальных асимптот нет
b) 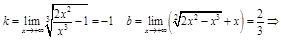
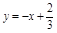
3. 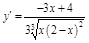
a) критические точки 1-го порядка: 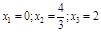

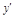 – + – –
– + – –
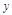 0 4/3 2 x
0 4/3 2 x
b) 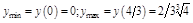
4. 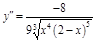
a) критические точки 2-го порядка: 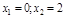

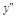 – – +
– – +
b) 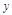
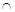 0
0 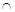 2
2 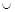 x
x
c) 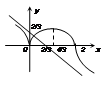 точка перегиба:
точка перегиба: 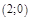
5. 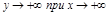 ,
, 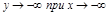
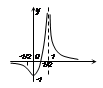 ПР. 3.
ПР. 3. 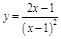
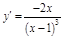 ;
; 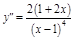 ;
; 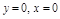 – ас-ты,
– ас-ты, 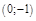 – min,
– min, 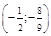 – перегиб.
– перегиб.
Пр. 4. 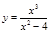
1.
a) 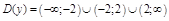
b) 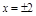 – т. разрыва 2-го рода
– т. разрыва 2-го рода
c) нечетная
d) непериодическая
e) 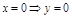
2.
a) 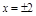 – верт. асимптоты,
– верт. асимптоты, 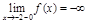 ,
, 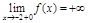 ,
, 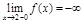 ,
, 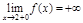 .
.
b) 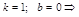
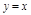
3. 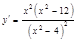
a) 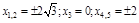

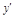 + – – – – +
+ – – – – +
b) 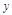
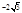 -2 0 2
-2 0 2 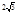 x
x
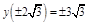
c) 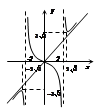
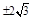 – точки максимума и минимума;
– точки максимума и минимума; 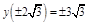
4. 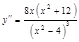
a) 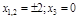



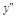 – + – +
– + – +
b) 
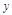
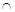 -2
-2 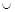 0
0  2
2 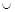 x
x
c) точка перегиба: 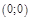
5. 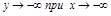 ,
, 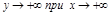
________________________________________________________
§ 5. Глобальный экстремум. на практику!
Если 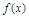 непрерывна на
непрерывна на 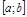 , то своего наибольшего (наименьшего) значения она может достигать либо в точке локального экстремума, принадлежащей
, то своего наибольшего (наименьшего) значения она может достигать либо в точке локального экстремума, принадлежащей 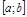 , либо на конце отрезка (проиллюстрировать на рис.).
, либо на конце отрезка (проиллюстрировать на рис.).
Правило: чтобы найти наибольшее и наименьшее значения 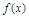 на отрезке
на отрезке 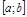 (области определения), надо:
(области определения), надо:
1) найти все точки локальных экстремумов 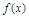 на
на 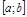 (или критические точки первого порядка), вычислить в них
(или критические точки первого порядка), вычислить в них 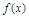 ;
;
2) вычислить 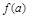 и
и 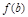 (значения на концах области определения);
(значения на концах области определения);
3) из всех полученных значений 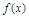 выбрать наибольшее и наименьшее.
выбрать наибольшее и наименьшее.
Пр. Найти наибольшее и наименьшее значения 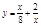 на отрезке
на отрезке 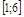 . Ответ:
. Ответ: 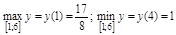 .
.
 2015-01-21
2015-01-21 401
401







