Т. 1. О производной монотонной ф-и:
1) Если 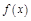 диф-ма на
диф-ма на 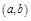 и возр-ет (убывает) на
и возр-ет (убывает) на 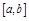 , то
, то 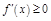
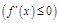
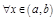 .
.
2) Если 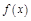 диф-ма на
диф-ма на 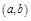 , непрерывна на
, непрерывна на 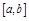 и
и 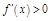
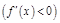
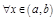 , то
, то 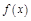 возрастает (убывает) на
возрастает (убывает) на 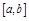 .
.
Д-во 1) 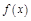 – возр-ет на
– возр-ет на 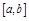 , возьмем
, возьмем 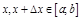 ,
, 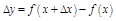 .
. 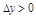 при
при 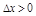 и
и 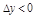 при
при 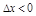
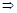 в обоих случаях
в обоих случаях 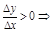
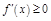 .
.
Д-во 2) 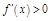 на
на 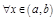 . Возьмем
. Возьмем 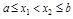 . По т. Лагранжа о конечных приращениях имеем:
. По т. Лагранжа о конечных приращениях имеем: 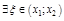 :
: 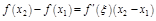 . Т.к.
. Т.к. 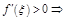
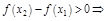
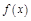 возр-ет на
возр-ет на 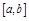 .
. 
Геом. смысл т еоремы: Если 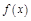 возр. на
возр. на 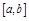 , то касательная к кривой
, то касательная к кривой 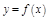 в любой точке отрезка
в любой точке отрезка 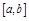 образует с Ox острый угол:
образует с Ox острый угол: 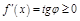 .
.
Т. 2. Теорема Ферма (необходимое условие экстремума):
Если 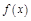 опр. и диф. на
опр. и диф. на 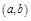 и имеет в т.
и имеет в т. 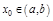 экстремум, то
экстремум, то 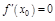 .
.
Д-во. Пусть т.  – т. лок. max.
– т. лок. max. 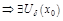 :
: 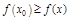
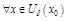 . Пусть
. Пусть 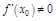 . Тогда
. Тогда 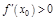 или
или 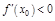 .
.
_______________________________________________________
а) если 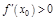 , то
, то 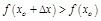 при нек.
при нек. 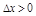 , т.о. ф. возр. в нек. окр. т.
, т.о. ф. возр. в нек. окр. т.  (м. считать в
(м. считать в 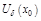 ), тогда для
), тогда для 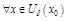 и
и 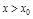
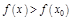 ;
;
б) если 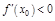 , то
, то 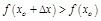 при нек.
при нек. 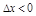 , т.о. ф. убыв. в нек. окр. т.
, т.о. ф. убыв. в нек. окр. т.  (м. считать в
(м. считать в 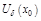 ), тогда для
), тогда для 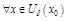 и
и 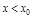
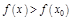 ;
;
Т.е. т.  не явл-ся т. лок. max, т.е. противоречие.
не явл-ся т. лок. max, т.е. противоречие. 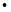
Вывод: в точках, в к-х 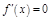 может быть экстремум (а может и не быть!).
может быть экстремум (а может и не быть!).
Зам. 1: 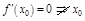 – точка локального экстремума.
– точка локального экстремума.
Зам. 2: Ф-ция 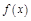 может иметь экстремум в т.
может иметь экстремум в т.  , в которых
, в которых 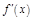 не сущ. или равна
не сущ. или равна 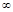 .
.
ПР. 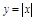 . В т.
. В т. 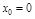 ф-ция не диф-ма, но имеет мин.
ф-ция не диф-ма, но имеет мин.
ПР. 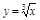 . В т.
. В т. 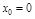
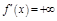 , но экстр. в ней нет.
, но экстр. в ней нет.
Опр. Точки ф-ции, в к-х 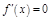 или терпит разрыв, наз-ся критическими точками 1-го рода.
или терпит разрыв, наз-ся критическими точками 1-го рода.
Очевидно, что не во всякой критической точке ф-ция имеет экстремум. Однако, если в т. ф-ция имеет экстремум, то это обязательно критическая точка.
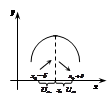 Т.3. Первое достаточное условие существования экстремума: Пусть
Т.3. Первое достаточное условие существования экстремума: Пусть 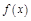 непр-на в нек.
непр-на в нек. 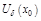 и диф-ма в ней за исключением, б.м., т.
и диф-ма в ней за исключением, б.м., т.  . Если при переходе ч/з т.
. Если при переходе ч/з т. 
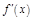 меняет знак, то
меняет знак, то  - т. лок. экстр.
- т. лок. экстр. 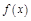 .
.
Д-во. Обозначим 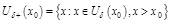 ;
;
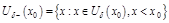 .
.
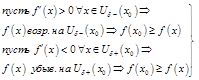
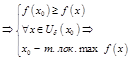
Аналогично м. д-ть, что если 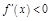 ,
, 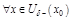 и
и 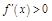 ,
, 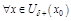
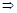
 – т. лок. минимума
– т. лок. минимума 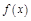 .
.
Т.о., если при переходе слева направо ч/з т. 
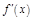 меняет знак с + на –, то
меняет знак с + на –, то  – т. лок. max; с – на +, то
– т. лок. max; с – на +, то  – т. лок. min.
– т. лок. min.
ПР. 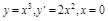 – кр. т. 1-го рода, но
– кр. т. 1-го рода, но 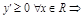 экстр. нет.
экстр. нет.
ПР. 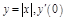 не сущ.
не сущ. 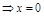 – кр.т.;
– кр.т.; 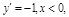
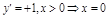 – т. min.
– т. min.
ПР. 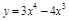 . Найти экстремумы.
. Найти экстремумы.
Правило отыскания локальных экстремумов 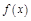 :
:
1. Найти 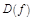 .
.
2. Найти критические точки 1-го порядка.
3. Нанести на числ. ось критические точки 1-го порядка и определить знаки 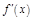 на интервалах, на которые кр. точки 1-го порядка разбили
на интервалах, на которые кр. точки 1-го порядка разбили 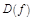 .
.
4. Выделить кр. точки, при переходе ч/з которые 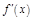 меняет знак.
меняет знак.
5. Выч-ть значения 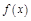 в т. экстр.
в т. экстр.
ПР. Предприятие производит x ед. продукции в месяц. Зависимость финансовых накоплений предприятия от объема выпуска продукции выражается формулой: 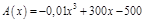 . Определить, при каком объеме выпуска продукции фин. накопления предприятия максимальны.
. Определить, при каком объеме выпуска продукции фин. накопления предприятия максимальны.
_______________________________________________________
Реш. 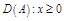 ;
; 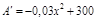 ;
; 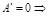
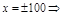
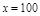 .
. 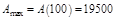 .
.
Т.4. Второе достаточное условие существования экстремума: Если ф. 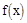 в нек.
в нек. 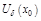 имеет непр. 1-ю и
имеет непр. 1-ю и
2-ю производные и 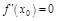 ,
, 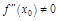 , то в т.
, то в т. 
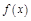 имеет экстремум, причем max, если
имеет экстремум, причем max, если 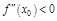 , и min, если
, и min, если 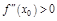 .
.
Д-во. Пусть 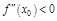
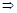 в силу непр.
в силу непр. 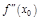 ,
, 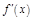 убывает в нек. окр. т.
убывает в нек. окр. т.  . Но
. Но 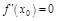
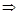 в этой окр.
в этой окр. 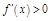 при
при 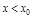 и
и 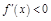 при
при 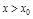
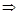
 – т. лок. max. (
– т. лок. max. (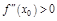 д-ть сам.!).
д-ть сам.!).
Зам. 1: Если 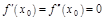 , то про наличие экстремума в точке
, то про наличие экстремума в точке  ничего сказать нельзя.
ничего сказать нельзя.
Зам. 2: Если 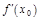
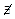 , то
, то 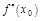 тоже
тоже 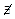 и вопрос о существовании экстремума решается по первому достаточному условию.
и вопрос о существовании экстремума решается по первому достаточному условию.
ПР. 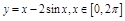 .
. 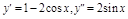 .
. 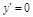 при
при 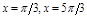 .
. 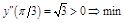 ,
, 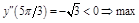 .
.
Зам.3. Достаточное условие 2 м. обобщить:
Пусть 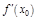 =
= 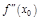 =…=
=…= 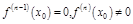 .
.
Если n -чет., то экстремум есть; если n - неч., то экстремума нет. При этом, если 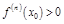 , то min; если
, то min; если 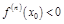 – max.
– max.
 §2. Направление выпуклости. Точки перегиба.
§2. Направление выпуклости. Точки перегиба.
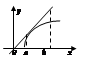 Опр. Непрерывная кривая наз-ся выпуклой вверх (выпуклым) на
Опр. Непрерывная кривая наз-ся выпуклой вверх (выпуклым) на 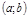 , если все ее точки лежат ниже любой ее касательной на этом интервале.
, если все ее точки лежат ниже любой ее касательной на этом интервале.
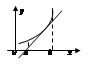 Опр. Непрерывная кривая наз-ся выпуклой вниз (вогнутой) на
Опр. Непрерывная кривая наз-ся выпуклой вниз (вогнутой) на 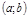 , если все ее точки лежат выше любой ее касательной на этом интервале.
, если все ее точки лежат выше любой ее касательной на этом интервале.
Выпуклая вверх кривая иногда наз-ся выпуклой, выпуклая вниз – вогнутой.
Т. 5. Достаточное условие выпуклости графика функции: Если ф-ция 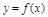 имеет
имеет 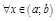
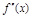 и
и 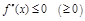
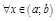 , то график ф-ции
, то график ф-ции 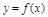 является выпуклой вверх (вниз) кривой на
является выпуклой вверх (вниз) кривой на 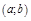 .
.
 Геометрическое пояснение:
Геометрическое пояснение: 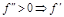 возрастает, значит,
возрастает, значит, 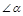 увел-ся.
увел-ся.

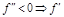 убывает, значит,
убывает, значит, 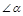 умен-ся.
умен-ся.
Правило для запоминания:
Д-во: ( можно не давать ). По опр., все т. кривой на 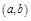 должны лежать ниже кас-ной в этих т., т.е. ордината любой т.
должны лежать ниже кас-ной в этих т., т.е. ордината любой т. 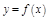 меньше ординаты кас-ной при одном и том же x.
меньше ординаты кас-ной при одном и том же x.
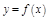 ;
; 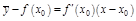
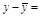
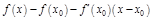 , к разности
, к разности 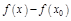
_______________________________________________________
запишем Т. Лагранжа: 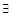 точка с:
точка с: 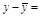
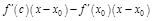
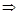
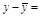
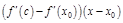 , по т Лагранжа
, по т Лагранжа 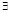 т.
т. 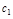 :
: 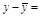
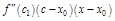 .
.
а) 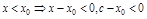 , но
, но 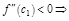
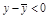 .
.
б) 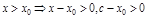 , но
, но 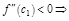 .
. 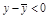
Аналог. д-ся дост. усл. вып. вниз. (сам.!)
ПР. 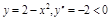 …кривая выпукла вверх.
…кривая выпукла вверх.
Опр. Точка кривой, при переходе через которую кривая меняет направление выпуклости, наз-ся точкой перегиба.
Касательная в т. перегиба пересекает график!!! (+ рис.)
Т. 6. Необходимое условие перегиба: Если 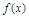 определена и дважды дифференцируема в некоторой окрестности точки
определена и дважды дифференцируема в некоторой окрестности точки  и
и 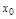 – точка перегиба, то
– точка перегиба, то 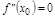 . (+ рис.)
. (+ рис.)
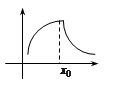 Замечание 1:
Замечание 1: 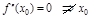 – точка перегиба.
– точка перегиба.
Зам. 2: В точке перегиба может  не сущ. или
не сущ. или 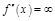 (см. рис.).
(см. рис.).
Опр. Точки, в к-х 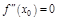 , либо
, либо 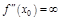 , либо
, либо 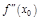 не сущ-ет, наз-ся критическими точками 2-го рода.
не сущ-ет, наз-ся критическими точками 2-го рода.
Т. 7. Достаточное условие перегиба: Пусть 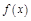 непр-на в нек.
непр-на в нек. 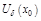 и дважды диф-ма в ней за исключением, б.м., т.
и дважды диф-ма в ней за исключением, б.м., т.  . Если при переходе ч/з т.
. Если при переходе ч/з т. 
 меняет знак, то
меняет знак, то  – абсцисса точки перегиба графика ф-ции
– абсцисса точки перегиба графика ф-ции 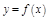 .
.
ПР. 1. 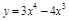 ,
, 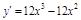 ,
, 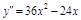 .
.
ПР. 2. 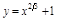 ;
; 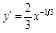 ;
; 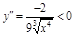
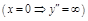 .
.
ПР. 3. 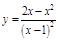 ;
; 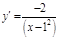 ;
; 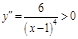
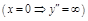 .
.
 2015-01-21
2015-01-21 476
476







