2015-01-21
2957
Рассмотрим свободно движущуюся со скоростью v частицу массой т. Вычислим для нее фазовую и групповую скорости волн де Бройля. Фазовая скорость, согласно (154.8),
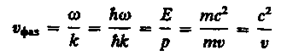(214.1)
(E = ℏw и p = ℏk, где k = 2p/ l — волновое число). Так как c > v, то фазовая скорость волн де Бройля больше скорости света в вакууме (фазовая скорость волн может быть как меньше, так и больше с в отличие от групповой скорости волн (см. § 155)). Групповая скорость, согласно (155.1),
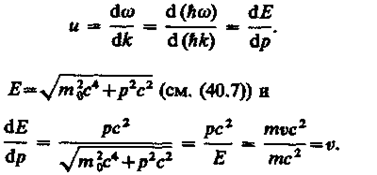
Следовательно, групповая скорость волн де Бройля равна скорости частицы.
Групповая скорость фотона
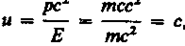
т. е. равна скорости самого фотона.
Волны де Бройля испытывают дисперсию (см. § 154). Действительно, подставив в выражение (214.1) vфаз = E/pформулу (40.7)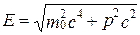 
, увидим, что скорость волн де Бройля зависит от длины волны. Это обстоятельство сыграло в свое время большую роль в развитии положений квантовой механики. После установления корпускулярно-волнового дуализма делались попытки связать корпускулярные свойства частиц с волновыми и рассматривать частицы как «узкие» волновые пакеты (см. § 155), «составленные» из волн де Бройля. Это позволяло как бы отойти от двойственности свойств частиц. Такая гипотеза соответствовала локализации частицы в данный момент времени в определенной ограниченной области пространства. Аргументом в пользу этой гипотезы являлось и то, что скорость распространения центра пакета (групповая скорость) оказалась, как показано выше, равной скорости частицы. Однако подобное представление частицы в виде волнового пакета (группы волн де Бройля) оказалось несостоятельным из-за сильной дисперсии волн де Бройля, приводящей к «быстрому расплыванию» (примерно 10-26 с!) волнового пакета или даже разделению его на несколько пакетов.
|
|
|
