Пусть заданы (рис. 1.24) длина стойки 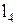 , угловые координаты входного звена 1 в трех положениях:
, угловые координаты входного звена 1 в трех положениях: 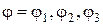 и соответствующие угловые координаты выходного звена 3:
и соответствующие угловые координаты выходного звена 3: 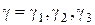 . Нужно найти длины звеньев
. Нужно найти длины звеньев 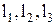 .
.
Рассмотрим векторный контур АВСДА, для которого в любом положении механизма 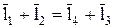 . Проецируя этот контур на координатные оси X и У, имеем:
. Проецируя этот контур на координатные оси X и У, имеем:
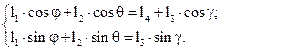 | (1.4.) (1.5.) |
Исключим угол 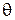 , решив уравнения (1.4) и (1.5) относительно слагаемых, содержащих
, решив уравнения (1.4) и (1.5) относительно слагаемых, содержащих 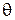 , возведя полученные равенства в квадрат и сложив их:
, возведя полученные равенства в квадрат и сложив их:
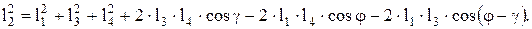
После деления на 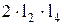 и замены текущих значений углов
и замены текущих значений углов 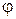 и
и 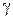 на заданные
на заданные 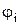 и
и 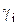 (индекс i=1, 2, 3), получим систему трех линейных уравнений:
(индекс i=1, 2, 3), получим систему трех линейных уравнений:
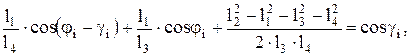
или
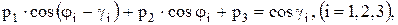 | (1.6) |
где неизвестными являются безразмерные параметры:
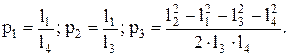 | (1.7) |
Из системы (1.6) находим, 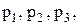 а затем согласно (1.7) находим искомые длины звеньев по формулам:
а затем согласно (1.7) находим искомые длины звеньев по формулам:
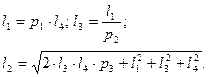
Задачу синтеза шарнирного четырёхзвенника по трем положениям выходного звена и соответствующим углам поворота входного звена решают методом обращения движения. В этом случае заданы длины звеньев 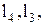 координаты выходного звена 3 в трех положениях
координаты выходного звена 3 в трех положениях 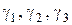 и углы поворота входного звена
и углы поворота входного звена 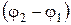 и
и 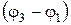 . Требуется найти длины звеньев
. Требуется найти длины звеньев 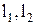 и начальную угловую координату (в положение 1)
и начальную угловую координату (в положение 1) 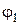 .
.
Положение шарнира В по заданным условиям находят путем сообщения всему механизму относительно центра А угловой скорости 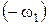 . В результате звено АВ в системе координат
. В результате звено АВ в системе координат 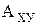 станет неподвижной, а вместо него в противоположном направлении будет вращаться стойка
станет неподвижной, а вместо него в противоположном направлении будет вращаться стойка 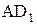 (рис. 1.25). Для второго и третьего положения механизма угловыми координатами стойки по отношению к оси абсцисс будут -
(рис. 1.25). Для второго и третьего положения механизма угловыми координатами стойки по отношению к оси абсцисс будут - 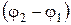 и -
и - 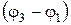 . Положение шарнира С является определенным по отношению к стойке и найдется путем построения заданных углов
. Положение шарнира С является определенным по отношению к стойке и найдется путем построения заданных углов 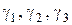 (точки
(точки 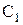 ,
, 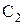 ,
, 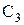 ). Длина шатуна ВС для трех заданных положений одна и та же
). Длина шатуна ВС для трех заданных положений одна и та же 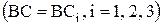 , поэтому точки
, поэтому точки 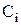 должны находиться на окружности, описанной из центра В. Следовательно, положение неизвестной точки В найдется, если точки
должны находиться на окружности, описанной из центра В. Следовательно, положение неизвестной точки В найдется, если точки 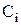 соединить двумя прямыми
соединить двумя прямыми 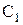
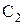 и
и 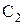
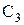 , провести через их середины
, провести через их середины 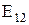 ,
, 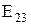 перпендикуляры и найти точку пересечения последних. При аналитическом решении для получения формул координат
перпендикуляры и найти точку пересечения последних. При аналитическом решении для получения формул координат 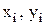 точек
точек 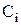 кинематическая цепь
кинематическая цепь 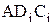 представленного в виде суммы двух векторов
представленного в виде суммы двух векторов 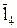 и
и 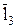 . Координаты точек
. Координаты точек 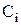 определяются проекциями указанной векторной цепи на координатные оси:
определяются проекциями указанной векторной цепи на координатные оси:
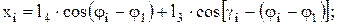

Координаты точки В найдем из системы уравнений окружности, описанной из центра В радиусом 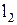 :
:
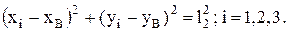 | (1.8) |
Система (1.8) трех уравнений с тремя неизвестными 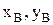 и
и 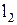 после несложных преобразований для исключения
после несложных преобразований для исключения 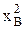 и
и 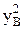 сводится к линейной.
сводится к линейной.
По координатам 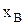 и
и 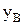 определяют искомые параметры кинематической схемы механизма:
определяют искомые параметры кинематической схемы механизма:
длину входного звена 1:
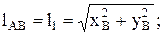
длину шатуна ВС:
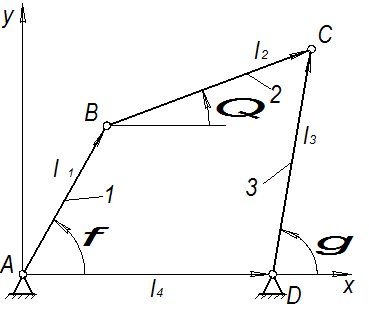 | |
| Рис. 1.24 | |
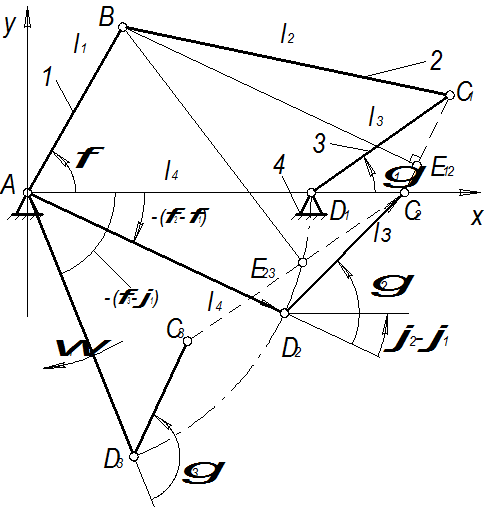 | |
| Рис. 1.25 |
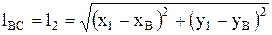
(как расстояние между точками 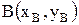 и
и 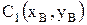 );
);
начальную угловую координату входного звена:
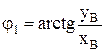
 2015-01-22
2015-01-22 1282
1282








