Реальная катушка (обмотка) любого электротехнического устройства обладает определенным активным сопротивлением r и индуктивностью L. Для удобства анализа таких цепей катушку обычно изображают в виде двух идеальных элементов — резистивного r и индуктивного L, соединенных последовательно (рис. 2.9, а). Используя выводы, вытекающие из анализа идеальных цепей, участок цепи с индуктивностью L будем рассматривать как участок, обладающий индуктивным сопротивлением хL. Уравнение напряжений, составленное по второму закону Кирхгофа для цепи с r и L, имеет вид
u = ur + uL.
Выразив напряжения ur и uL через ток i = Im sin ωt и сопротивления участков цепи r и хL, получим
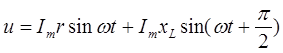
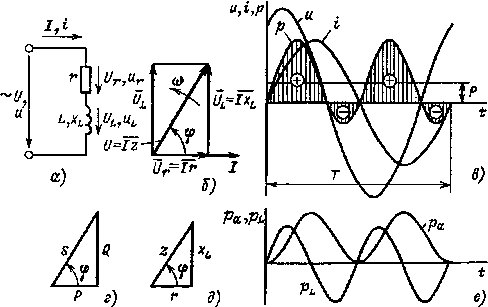
Рис. 2.9. Электрическая цепь, содержащая катушку индуктивности r и L (а), ее векторная диаграмма (б), графики мгновенных значений u, i, р (в), треугольники мощностей и сопротивлений (г, д), графики мгновенных значений рa, pL (e)
где ur = Imr sin ωt — напряжение на активном сопротивлении (активное напряжение), совпадающее по фазе с током; uL = ImxLsin (ωt + π/2) — напряжение на индуктивном сопротивлении (индуктивное напряжение), опережающее ток по фазе на 90°.
На векторной диаграмме (рис. 2.9, б) вектор Ūr совпадает с вектором тока, а вектор ŪL опережает вектор тока на 90°.
Из диаграммы следует, что вектор напряжения сети равен геометрической сумме векторов Ūr и ŪL:
Ū = Ūr + ŪL,
а его значение
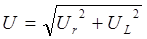
Выразив напряжения через ток и сопротивления, получим
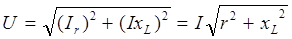
Последнее выражение представляет собой закон Ома цепи r, xL
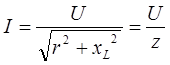
где 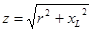 — полное сопротивление цепи, Ом.
— полное сопротивление цепи, Ом.
Из векторной диаграммы следует, что напряжение цепи r, L опережает по фазе ток на угол φ и его мгновенное значение
u = Um sin (ωt + φ)
Графики мгновенных значений напряжения в тока цепи изображены на рис. 2.9, в.
Угол сдвига по фазе φ между напряжением и вызванным им током определяют из соотношения
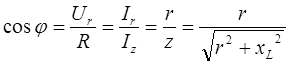 (2.15)
(2.15)
Как видно, cos φ и, следовательно, угол φ зависят только от параметров цепи r и xL.
Разделив стороны треугольника напряжений на ток, получим треугольник сопротивлений (рис. 2.9, д), Стороны треугольника сопротивлений представляют собой отрезки, а не векторы, так как сопротивления есть постоянные, не изменяющиеся синусоидально величины.
Мгновенная мощность цепи с r и L равна произведению мгновенных значений напряжения и тока:
р = ui = Im sin ωt Um sin (ωt + φ).
Средняя мощность за период
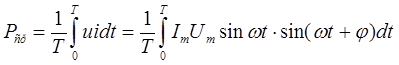
Выразив произведение синусов через разность косинусов, после почленного интегрирования получим
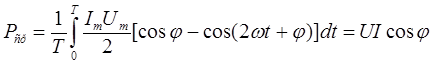 (2.16)
(2.16)
Подставив в (2.16) вместо cos φ его значение из (2.15), получим
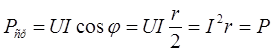 (2.17)
(2.17)
Из (2.17) вытекает, что среднее значение мощности в цепи с r и L есть активная мощность, которая выделяется в активном сопротивлении r в виде теплоты.
График мгновенной мощности изображен на рис. 2.9, в.
Для анализа энергетических процессов в цепи r, L мгновенную мощность удобно представить в виде суммы мгновенных значений активной pa = uri и реактивной (индуктивной) pL = uLi мощностей:
p = pa + pL.
Графики pa(t), pL(t) изображены на рис. 2.9, е. График pa(t) аналогичен графику для цепи с активным сопротивлением (см. § 2,4), а график pL(t) — для цепи с индуктивностью L (см. § 2.5).
Таким образом, энергетические процессы в цепи с r, L можно рассматривать как совокупность процессов, происходящих в цепях только с активным сопротивлением r и только с индуктивностью L.
Из графика pa(t) видно, что активная мощность непрерывно поступает из сети и выделяется в активном сопротивлении в виде теплоты. Она равна
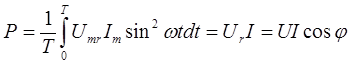
Мгновенная мощность рL, обусловленная энергией магнитного поля индуктивности, циркулирует между сетью и катушкой. Ее среднее значение за период равно нулю:
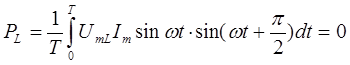
 2015-01-22
2015-01-22 3665
3665








