Нормаль в точке соприкосновения элементов высшей пары качения и скольжения делит линию центров на части. Обратно пропорциональные угловым скоростям.
Точка 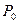 , делящая линию центров
, делящая линию центров 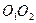 на части. Обратно пропорционально угловым скоростям, является мгновенным центром вращения в относительном движении звеньев 1 и 2.
на части. Обратно пропорционально угловым скоростям, является мгновенным центром вращения в относительном движении звеньев 1 и 2.
Расстояние a между точками 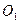 и
и 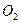 равно
равно

 (5.5)
(5.5)
Из равенства (5.4) и (5.5) следует, что радиусы  и
и  центроид равны
центроид равны
 , и
, и  (5.6)
(5.6)
Мгновенный центр вращения 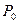 в теории зацеплений называется полюсом зацепления.
в теории зацеплений называется полюсом зацепления.
При переменном значении передаточной функции 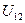 полюс зацепления
полюс зацепления 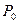 занимает на линии центров
занимает на линии центров 
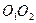 переменные положения. При постоянном значении
переменные положения. При постоянном значении 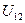 полюс зацепления располагается в одной и той же точке на прямой
полюс зацепления располагается в одной и той же точке на прямой 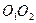 .
.
Если угловые скорости 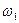 и
и 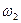 имеют разные знаки (см. рис 5.1,a), то
имеют разные знаки (см. рис 5.1,a), то  и полюс зацепления
и полюс зацепления 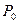 лежит между точками
лежит между точками 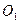 и
и 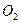 . Этот вид зацепления называется внешним. Если
. Этот вид зацепления называется внешним. Если 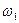 и
и 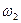 имеют одинаковый знак и полюс зацепления
имеют одинаковый знак и полюс зацепления 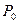 лежит вне отрезка
лежит вне отрезка 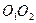 , то
, то 
 (зацепление внутреннее).
(зацепление внутреннее).
Основной закон зацепления формулируется так: для сохранения постоянства передаточного отношения зубчатого механизма необходимо, чтобы нормаль к зацепляющимся профилям зубьев в точке контакта всегда проходила на линии центров через одну и ту же точку 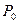 (полюс зацепления).
(полюс зацепления).
 2015-01-30
2015-01-30 285
285








