Определение минимального радиуса профиля кулачка

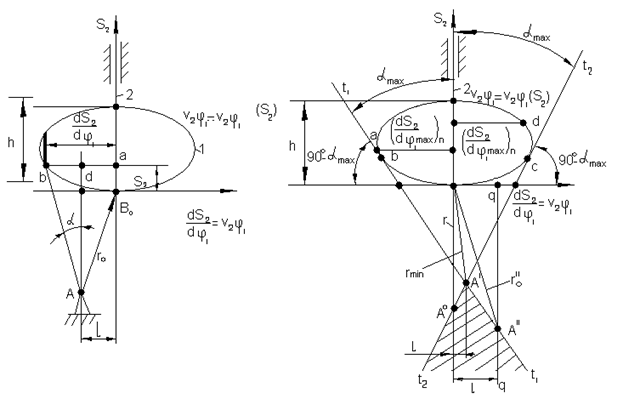
Рис.6.6. Определение угла давления по диаграмме аналога скорости в функции пути толкателя.

Рис.6.7. Графическое определение минимального радиуса профиля кулачка.

Величины углов давления для всего цикла движения кулачкового механизма могут быть определены графически с помощью следующего построения (рис.6.6). Построим кривую зависимости аналога скорости 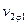от перемещения 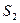. Перемещения 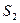будем откладывать от точки 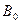, соответствующей нижнему начальному положению толкателя в направлении его движения, а аналоги скоростей 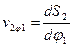- в перпендикулярном направлении. Тогда, если соединить какую либо точку в построенной кривой с осью вращения А кулачка, то из построения следует, что направление AB образует с осью 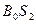угол давления .

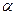В самом деле, из рис. 6.6 имеем

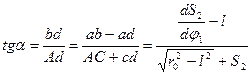(6.15)

т.е. условия (6.13) удовлетворяются. Решим обратную задачу об определении величины наименьшего радиус-вектора 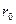кулачка, если задан закон движения 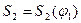толкателя 2, смещение 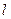и максимально допустимый угол давления 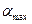. Для этого (рис.6.7) строим кривую, 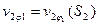как для фазы подъёма, так и для фазы опускания. Далее проводим к кривой 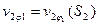касательные 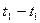и 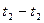под углам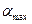и к оси 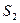. Точка 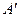пересечения этих касательных определит положение оси вращения кулачка, имеющего наименьший радиус-вектор 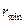. При выборе оси вращения в т. 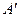получается вполне определённая величина смещения 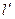. Если величина смещения 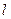задана, то, проводя прямую 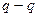на расстоянии 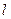от оси 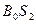, найдём т. 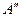пересечения этой прямой с касательной 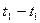. Если т. 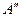выбрать за ось вращения кулачка, то наименьший радиус-вектор кулачка будет равен 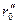. Если смещение 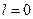, то мы получаем кулачковый механизм с центром вращения в т. 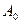и наименьший радиус-вектор кулачка равен 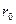. При выборе оси вращения кулачка в заштрихованной зоне в пределах угла 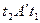, образуемого касательным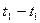и , и 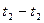всегда удовлетворяется условие, в соответствии с которым угол давления в любом положении механизма меньше заданного предельного угла давления 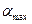. Точки касания b и c прямых 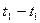и 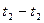с кривой 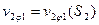не совпадают с точками a и d (рис.6.7), где значение 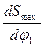достигают максимальных значений: 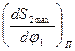для фазы подъёма и 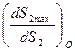для фазы опускания.