2015-03-07
597
Известны следующие параметры механизма: график перемещений толкателя (рис. 4.2), минимальный радиус кулачка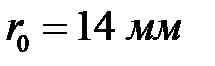 
, радиус ролика 
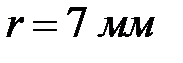, ход толкателя 
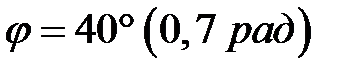, межосевое расстояние 
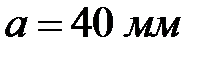, длина толкателя 
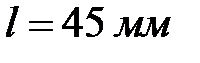, скорость кулачка 
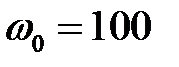1/с, направление вращения кулачка – против часовой стрелки.
Требуется построить профиль кулачка.
Выбираем масштабный коэффициент кулачкового механизма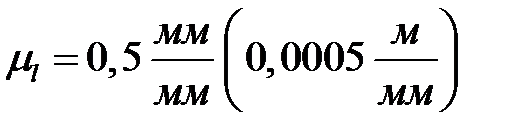 
. Это означает, что механизм изображается увеличенным в два раза.
Находим размеры на чертеже
, 
, 
,
.
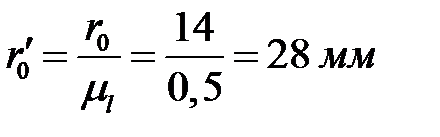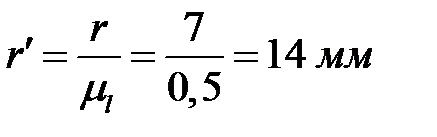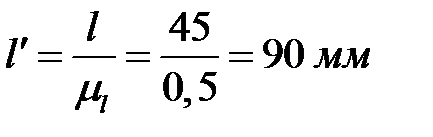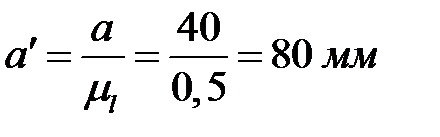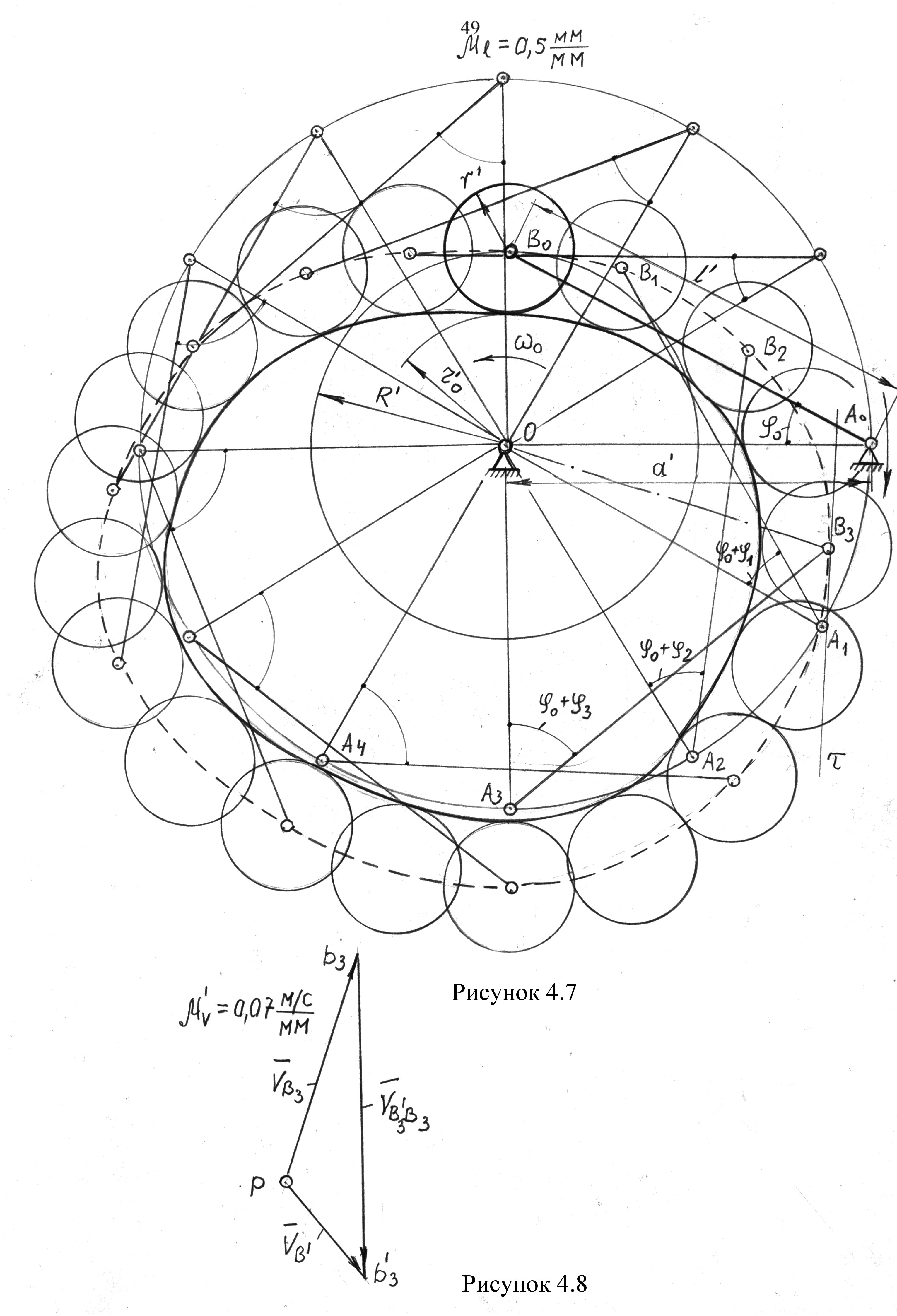
Из произвольной точки О (рис. 4.7) радиусом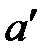 
, проводим окружность, которую делим на 12 частей, причем нумерацию точек 
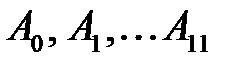ведем в направлении, обратном направлению вращения кулачка. Все эти точки соединяем с точкой 
. Вычисляем значения углов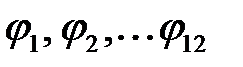 
из графика перемещений (рис. 4.2) по формуле
, 
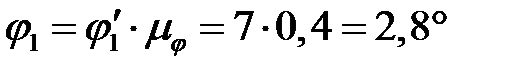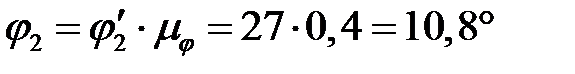и т.д.
Из точки О делаем засечку радиусом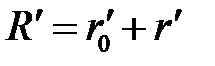 
, а из точки 
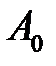– засечку радиусом 
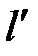, получая точку 
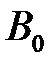. Замеряем угол 
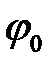. Из точки 
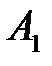проводим луч под углом 
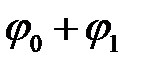, на котором откладываем величину 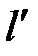. Получаем точку 
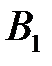. Из точки 
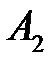проводим луч под углом 
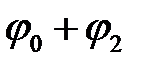, на котором находим точку 
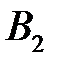и т.д. Точки 
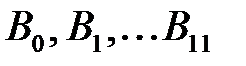соединяем плавной кривой, получая центровой (теоретический) профиль кулачка. Если расстояние между точками оказывается очень большим, то из кривой перемещений нужно вычислить промежуточное значение угла 
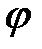и найти дополнительную точку В. На теоретическом профиле выбираем несколько точек (12 и более), из которых проводим окружности радиусом 
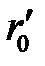. С внутренней стороны к окружностям проводим общую кривую касательную, которая служит рабочим (действительным) профилем кулачка. Действительный профиль кулачка, ролик и толкатель в одном из положений обводим толстыми линиями, а остальные построения — тонкими.
Для оценки точности построений найдем величину скорости толкателя в одном из положений, например, в третьем. Замеряем длину ординаты (рис. 4.1), которая в данном случае равна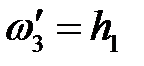 
. Следовательно,
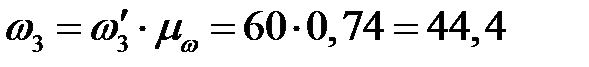1/с.
Построим план скоростей механизма для того же положения, используя векторное уравнение
,
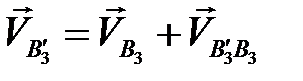где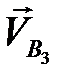 
– скорость точки 
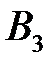, принадлежащей кулачку,
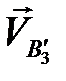– скорость точки 
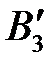, принадлежащей толкателю.
Скорость точки 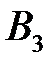определяем по формуле
,
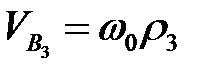где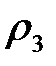 
– действительная величина радиуса центрового профиля кулачка.
Её можно найти через коэффициент, учитывая, что на чертеже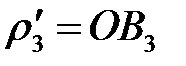 
. Следовательно 
.
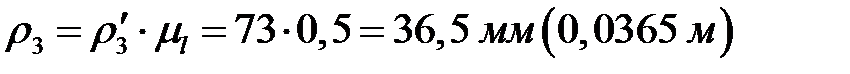Тогда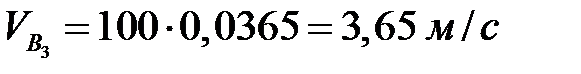 
.
Выбираем масштабный коэффициент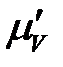 
для плана скоростей, изображая вектор 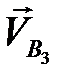отрезком 
.
.
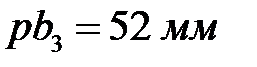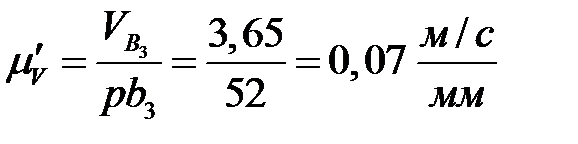Из полюса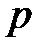 
(рис. 4.8) проводим вектор 
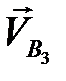перпендикулярно 
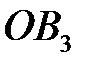в сторону вращения кулачка. В точке 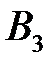центрового профиля проводим касательную 
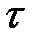, которую переносим в точку 
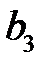на плане скоростей. Из полюса 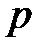проводим линию, перпендикулярную толкателю 
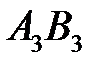. На пересечении ставим стрелки и букву 
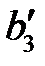. Получим векторы 
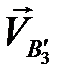и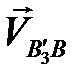 
. Замеряем длину вектора 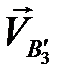и вычисляем его модуль
.
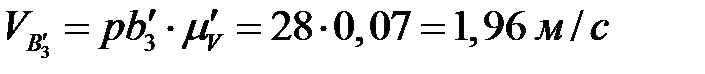Определяем угловую скорость толкателя
.
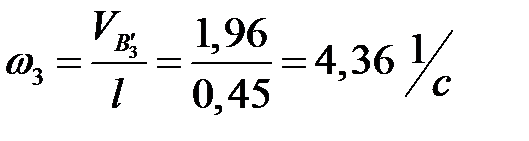После этого заключаем, что угловые скорости толкателя, полученные двумя способами, отличаются друг от друга незначительно, что свидетельствует о высокой точности построений.
