Алгоритмы закрашивания

Рассмотрим алгоритмы закрашивания произвольного контура, который уже нарисован в растре. Сначала определяются координаты произвольного пиксела, находящегося внутри очерченного контура фигуры. Цвет этого пиксела изменяем на нужный цвет заполнения. Потом проводится анализ цветов всех соседних пикселов. Если цвет некоторого соседнего пиксела не равен цвету границы контура или цвету заполнения, то цвет этого пиксела изменяется на цвет заполнения. Потом анализируется цвет пикселов, соседних с предшествующими. И так далее, пока внутри контура все пикселы не перекрасятся в цвет заполнения.

Пикселы контура образуют границу, за которую нельзя выходить в ходе последовательного перебора всех соседних пикселов. Соседними могут считаться только четыре пиксела (сосед справа, слева, сверху и снизу — четырехсвязность), или восемь пикселов (восьми-связность). Не всякий контур может считаться границей закрашивания, например, для восьмисвязного алгоритма (рис. 3. 36).

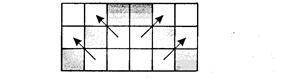
Рис. 3.36.Особенности восьмисвязного закрашивания - выход за границу контура на следующих

шагах закрашивания

Простейший алгоритм закрашивания. Для всех алгоритмов закрашивания нужно задавать начальную точку внутри контура с координатами х₀, у₀. Простейший алгоритм можно описать всего двумя шагами.

Алгоритм закрашивания линиями. Данный алгоритм получил широкое распространение в компьютерной графике. От приведенного выше простейшего алгоритма он отличается тем, что на каждом шаге закрашивания рисуется горизонтальная линия, которая размещается между пикселами контура. Алгоритм также рекурсивный, но поскольку вызов функции осуществляется для линии, а не для каждого отдельного пиксела, то количество вложенных вызовов уменьшается пропорционально длине линии. Это уменьшает нагрузку на стековую память компьютера и обеспечивает высокую скорость работы.

Пример работы алгоритма закрашивания линиями приведен на рис 3. 37.

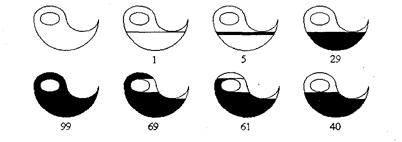
Рис. 3.37. Количество циклов LineFill

Алгоритмы заполнения, которые используют математическое описание контура

Математическим описанием контура фигуры может служить уравнение у =f(x) для контypa окружности, эллипса или другой кривой. Для многоугольника (полигона) контур задается множеством координат вершин (х_i, у_i). Возможны идругие формы описания контура. Общим для рассматриваемых ниже алгоритмов есть то, что для генерации точек заполнения не нужны предварительно сформированные в растре пикселы границы контура фигуры. Контур может вообще не рисоваться в растре ни до, ни после заполнения.

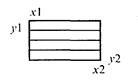
Рис. 3.38. Заполнение прямоугольника

Заполнение прямоугольников. Среди всех фигур прямоугольник заполнять наиболее просто. Если прямоугольник задан координатами противоположных углов, например, левого верхнего (х1, у1) и правого нижнего (х2, у2), тогда алгоритм может состоять в последовательном рисовании горизонтальных линий заданного цвета (рис. 3. 38).

Заполнение круга. Для заполнения круга можно использовать алгоритм вывода контура. В процессе выполнения этого алгоритма последовательно вычисляются координаты пикселов контура в границах одного октанта. Для заполнения следует выводить горизонтали, которые соединяют пары точек на контуре, расположенные симметрично относительно оси y (рис. 3.39, слева).

Так же можно создать и алгоритм заполнения эллипса.

Заполнение полигонов. Контур полигона определяется вершинами, которые соединены отрезками прямых — ребрами (рис. 3.39, справа). Это — векторная форма описания фигуры.

Рассмотрим один из наиболее популярных алгоритмов заполнения полигона. Его основная идея — закрашивание фигуры отрезками прямых линий. Удобней использовать горизонтали. Алгоритм представляет собою цикл вдоль оси у, в ходе этого цикла выполняется поиск точек пересечения линии контура с соответствующими горизонталями. Этот алгоритм получил название XY.

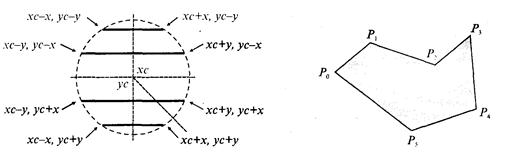
Рис. 3.39. Заполнение круга Пример полигона

В этом алгоритме использовано топологическое свойство контура фигуры. Оно состоит в том, что любая прямая линия пересекает любой замкнутый контур четное количество раз (рис. 3.40). Для выпуклых фигур точек пересечения с любой прямой всегда две.

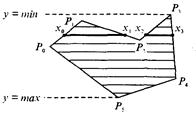
Рис. 3.40. Заполнение полигона

При нахождении точек пересечения горизонтали с контуром необходимо принимать во внимание особые точки. Если горизонталь имеет координату (у), совпадающую с координатой y_i вершины Р_i тогда надлежит анализировать то, как горизонталь проходит через вершину. Если горизонталь при этом пересекает контур, как, например, в вершинах Р₀ ли Р₄, то в массив записывается одна точка пересечения. Если горизонталь касается вершины контура (в этом случае вершина соответствует локальному минимуму или максимуму, как, например, в вершинах Р₁, Р₂, Р₃ или Р₅), тогда координата точки касания или Не записывается, или записывается в массив два раза. Это является условием четного количества точек пересечения, хранящихся в массиве {х_j}.

Процедура определения точек пересечения контура с горизонталью, учитывая анализ на локальный максимум, может быть достаточно сложной. Это замедляет работу. Радикальным решением для упрощения поиска точек пересечения может быть сдвиг координат вершин контура или горизонталей заполнения таким образом, чтобы ни одна горизонталь не попала в вершину.

Сдвиг можно выполнять разными способами, например, ввести в растр дробные координаты для горизонталей; y_min + 0. 5, y_min + 1. 5,..., y_min - 0. 5. Но такое упрощение процедуры нахождения точек пересечения приводит к некоторому искажению формы полигона.

Для определения координат (х) точек пересечения для каждой горизонтали необходимо перебирать все η ребер контура. Координата пересечения peбра p_i - p_k c горизонталью (у) равняется

x = x_i + (у_k - у)(х_к- х_i)/(у_k - у_i).

Количество тактов работы этого алгоритма:

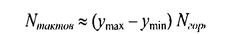
где y_max, y_min — диапазон координат y, Ν_гоρ — число тактов, нужных для одной горизонтали. Оценим величину Ν_гоρ как пропорциональную числу вершин

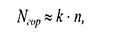
где к — коэффициент пропорциональности, n— число вершин полигона.

Возможна модификация приведенного алгоритма для ускорения его работы. Например, можно принять во внимание то, что каждая горизонталь обычно пересекает небольшое количество ребер контура. Поэтому, если при поиске точек пересечения делать предшествующий отбор ребер, которые находятся вокруг каждой горизонтали, то можно добиться уменьшения количества тактов работы с N_гор = к ∙ n до к^. ∙ n_р, где n_p — количество отобранных ребер. Например, разделим диапазон y_min -y_max пополам. Если для диапазона от y_min до y_ср, составить список ребер (или вершин), попадающих в этот диапазон, то в список будет включено приблизительно вдвое меньшее количество, чем для всего диапазона от y_min до y_max. Почему приблизительно — ибо это зависит от размещения вершин контура полигона. Таким образом, при работе алгоритма для каждой горизонтали в диапазоне от y_min до y_ср уже нужно не (к^. ∙ п) тактов, а (k · n/2).

Аналогично для диапазона у_ср-y_mах также можно составить список ребер, который также будет почти вдвое меньшим. Если принять, что подсчеты для каждой горизонтали теперь выполняются за вдвое меньшее количество тактов, а именно за (N_гор /2), то общее число тактов:

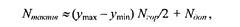
где Ν_доп — количество тактов, которые необходимы при создании списка ребер.

Такой способ повышения быстродействия заполнения полигонов эффективен для большого количества вершин. Контур можно делить не пополам, а на более мелкие части — соответственно повышается скорость.

Приведенные выше алгоритмы заполнения могут быть использованы не только для рисования фигур. На основе алгоритмов заполнения могут быть разработаны алгоритмы для других целей. Например, для определения площади фигуры (если считать площадь пропорциональной количеству пикселов заполнения). Или, например, алгоритм для поиска объектов по внутренней точке — эта операция часто используется в векторных графических редакторах.

Логическое условие будет определять стиль линии. Например, если условием будет четность значения С, то получим линию из разрозненных точек. Для рисования пунктирной линии можно анализировать остаток от деления С на S. Например, если рисовать пикселы линии только при С mod S < S/2, то получим пунктирную линию с длиной штрихов S/2. шаг штрихов — S.

При выводе полилиний, а также сплайновых кривых, аппроксимируемых прямолинейными отрезками, необходимо предотвратить обнуление значения счетчика в начале каждого отрезка и обеспечить продолжение непрерывного прироста вдоль всей сложной линии. Иначе будут нестыковки пунктира. Использование переменной-счетчика затруднено при генерации пунктирных линий в алгоритмах, которые используют симметрию, например, при выводе окружности или эллипса. Здесь необходимо обеспечивать стыковку пунктира на границах октантов или квадрантов.