Определение. Вектор 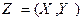 , компоненты Х и Y которого являются случайными величинами, называется случайным вектором или двумерной случайной величиной.
, компоненты Х и Y которого являются случайными величинами, называется случайным вектором или двумерной случайной величиной.
Пример. Пусть Х – рост человека, Y – вес человека. Тогда 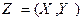 – (непрерывная) двумерная случайная величина.
– (непрерывная) двумерная случайная величина.
Пример. Пусть Х и Y – числа попаданий в мишень первого и второго стрелков (соответственно). Тогда 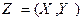 – (дискретная) двумерная случайная величина.
– (дискретная) двумерная случайная величина.
Сравнивая между собой одномерную (см. выше темы 3, 4) и двумерную случайные величины, заметим, что, если результат измерения первой – точка на прямой, то результат измерения второй – точка плоскости.
Определение. Закон распределения одной из переменных при фиксированном значении другой называется условным распределением.
Определение. Связь между переменными называется статистической, если каждому значению одной переменной ставится в соответствие условное распределение другой переменной.
Отметим, что задание двумерной случайной величины равносильно заданию статистической связи между переменными.
Рассмотрим сначала двумерную дискретную случайную величину.
По аналогии с одномерным случаем, закон распределения двумерной дискретной случайной величины задается с помощью таблицы вида:
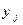 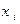 | 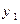 | … | 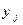 | … | 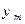 |
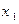 | 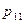 | … | 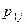 | … | 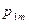 |
| … | … | … | … | … | … |
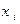 | 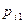 | … | 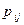 | … | 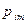 |
| … | … | … | … | … | … |
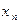 | 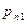 | … | 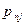 | … | 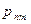 |
где
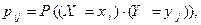
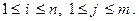
По аналогии с основным свойством закона распределения одномерной случайной величины, справедливо равенство
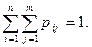
Приведенная таблица называется совместным законом распределения случайных величин Х и Y.
Пример #. Совместный закон распределения случайных величин Х и Y имеет вид:
 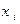 | ||
| 0,1 | 0,2 | |
| 0,3 | 0,4 |
Найти математическое ожидание случайной величины Х.
Решение. Прежде всего найдем закон распределения случайной величины Х. Так как
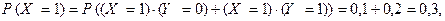
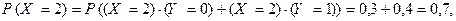
то закон распределения Х имеет вид:
| X: | 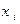 | ||
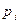 | 0,3 | 0,7 |
Тогда
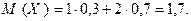
Оставляем читателю в качестве упражнения проверку того, что закон распределения случайной величины Y имеет вид:
| Y: | 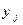 | ||
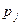 | 0,6 | 0,4 |
и 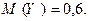
Определение. Связь между переменными называется функциональной, если каждому значению из области определения одной переменной поставлено в соответствие однозначно определенное значение другой переменной.
Примерами такого вида связи изобилует курс математического анализа: 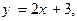
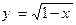 ,
, 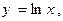
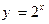 и т.д. и т.д.
и т.д. и т.д.
Определение. Функциональная связь между значениями одной переменной и условными математическими ожиданиями другой переменной называется корреляционной.
Определение. График корреляционной зависимости называется линией регрессии.
Корреляционные зависимости бывают двух видов (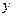 по
по 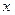 и
и 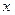 по
по 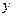 ) в зависимости от того, которая из переменных выполняет роль аргумента:
) в зависимости от того, которая из переменных выполняет роль аргумента: 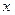 или
или 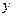 . Соответственно,
. Соответственно, 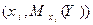 – точки корреляционной зависимости
– точки корреляционной зависимости 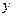 по
по 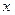 и
и 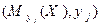 – точки корреляционной зависимости
– точки корреляционной зависимости 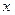 по
по 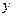 .
.
Пример. По совместному закону распределения из предыдущего примера (Пример #) найти корреляционную зависимость 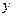 по
по 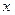 .
.
Решение. Применяя теорему умножения вероятностей, получаем
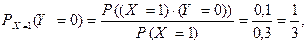
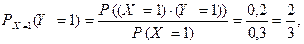

где вероятности, стоящие в числителях последних дробей, берутся из таблицы совместного закона распределения Примера #, вероятность 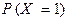 найдена в том же примере. Таким образом, условное распределение случайной величины Y при
найдена в том же примере. Таким образом, условное распределение случайной величины Y при 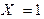 имеет вид:
имеет вид:
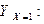 | 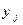 | ||
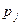 | 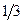 | 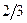 |
По этому закону распределения находим условное математическое ожидание:
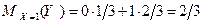 .
.
Аналогично получаем:
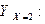 | 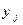 | ||
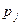 | 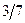 | 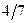 |
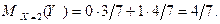
Собирая вместе полученные результаты, запишем корреляционную зависимость 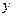 по
по 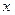 в виде следующей таблицы:
в виде следующей таблицы:
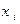 | ||
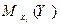 | 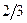 | 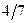 |
Упражнение. По совместному распределения Примера # убедиться, что корреляционная зависимость 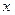 по
по 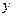 имеет вид:
имеет вид:
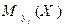 | 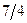 | 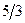 |
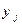 |
Рассмотрим теперь непрерывную двумерную случайную величину.
Определение. Функция 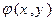 называется плотностью распределения непрерывной двумерной случайной величины
называется плотностью распределения непрерывной двумерной случайной величины 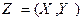 , если для произвольных чисел
, если для произвольных чисел 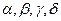
(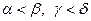 ) вероятность того, что в произвольном испытании значение случайной величины Z попадает в прямоугольник
) вероятность того, что в произвольном испытании значение случайной величины Z попадает в прямоугольник 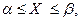
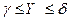 вычисляется по формуле
вычисляется по формуле
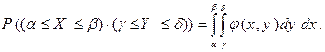
Условные плотности распределения определяются формулами:
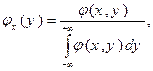
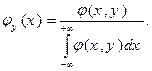
Соответственно, условные математические ожидания тогда вычисляются по формулам:
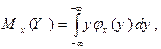
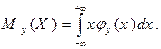
 2015-01-30
2015-01-30 1764
1764
