Парадокс нулевой вероятности

Теорема. Для непрерывной случайной величины вероятность принять произвольное числовое значение равно нулю.

Доказательство. Пусть 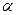– произвольное число. События 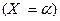и 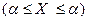– равны, поэтому, по определению плотности распределения, получаем

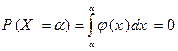
(см. свойства определенного интеграла).

Из парадокса нулевой вероятности вытекает, что для любой непрерывной случайной величины вероятности попадания в произвольный отрезок числовой оси или в соответствующий полуинтервал (интервал) равны между собой, т.е. справедливо

Следствие. Пусть Х непрерывная случайная величина и 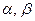– произвольные числа. Тогда верно следующее равенство

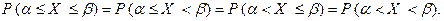
Доказательство. Очевидно, что

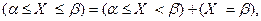
причем события 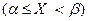и 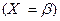– несовместны. Используя последнее равенство и теорему сложения вероятностей для несовместных событий, получаем

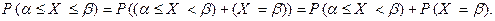
Но, согласно парадоксу нулевой вероятности, 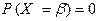.Тем самым доказано первое из трех равенств Следствия.

Доказательство оставшихся двух равенств мы оставляем читателю в качестве упражнения.