1. Если боковая поверхность правильной четырехугольной призмы равна 40 см2, а полная 90 см2, то высота призмы равна:
1) 5 см 2) 4 см 3) 2 см 4) 3 см 5) 10 см.
2. Высота правильной треугольной пирамиды равна равна 6 см. На расстоянии 3 см от вершины проведена плоскость, параллельная основанию. Площадь полученного сечения равна 5 см2. Тогда объем данной пирамиды равен:
1) 40 см2 2) 120 см2 3) 20 см2 4) 25 см2 5) 60 см2.
3. Если площадь основания правильного параллелепипеда равна 9 см2, а его полная поверхность равна 66 см2, то объем параллелепипеда равен:
1) 40 см3 2) 48 см3 3) 36 см3 4) 32 см3 5) 64 см3.
4. В основание правильной четырехугольной пирамиды вписан круг радиуса 2 см. Боковые грани составляют с плоскостью основания углы 60º. При этих условиях полная поверхность пирамиды равна:
1) 48 см2 2) 32 см2 3) 64 см2 4) 24 см2 5) 36 см2.
5. Около основания правильной шестиугольной призмы описана окружность радиуса 3 см. Высота призмы 4 см. Тогда площадь боковой поверхности призмы равна:
1) 84 см2 2) 36 см2 3) 72 см2 4) 54 см2 5) 42 см2.
6. В основании пирамиды лежит треугольник со сторонами 6 см, 8 см и 10 см. Все боковые грани образуют с основанием углы 60º. В этих условиях площадь полной поверхности пирамиды равна:
1) 72 см2 2) 64 см2 3) 48 см2 4) 56 см2 5) 88 см2.
7. В основании пирамиды лежит прямоугольный треугольник с катетами 6 см и 8 см. Объем пирамиды равен 40 см3. Все боковые ребра наклонены к плоскости основания под одинаковым углом. Этот угол равен:
1) 45º 2) 30º 3) 60º 4) 15º 5) 22º15´.
8. объем правильной треугольной призмы равен 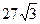 . Радиус окружности, описанной около основания равен 2. Найти высоту призмы.
. Радиус окружности, описанной около основания равен 2. Найти высоту призмы.
1) 6 2) 8 3) 15 4) 9 5) 12.
9. Объем куба равен 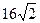 . Найти радиус окружности, описанной вокруг грани куба:
. Найти радиус окружности, описанной вокруг грани куба:
1) 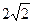 2) 3 3)
2) 3 3) 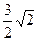 4) 2 5)
4) 2 5) 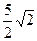 .
.
 2015-01-30
2015-01-30 1120
1120








