«ряды»
1. Доказать сходимость ряда и найти его сумму.
2. Исследовать сходимость знакоположительных рядов.
3. Исследовать на сходимость и абсолютную сходимость ряды.
4. Найти область сходимости степенного ряда.
5. Разложить функцию 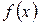 а) в ряд Тейлора в окрестности точки
а) в ряд Тейлора в окрестности точки 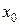 ; б) в ряд Маклорена. Найти область сходимости полученного ряда к этой функции. Вычислить приближенно число а с точностью
; б) в ряд Маклорена. Найти область сходимости полученного ряда к этой функции. Вычислить приближенно число а с точностью 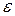 .
.
1.1 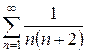
| 1.2 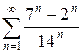
|
1.3 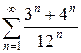
| 1.4 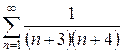
|
1.5 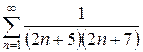
| 1.6 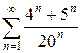
|
1.7 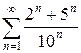
| 1.8 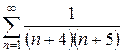
|
1.9 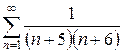
| 1.10 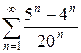
|
1.11 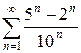
| 1.12 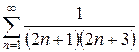
|
1.13 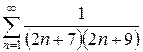
| 1.14 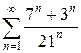
|
1.15 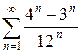
| 1.16 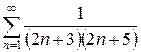
|
1.17 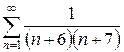
| 1.18 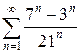
|
1.19 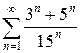
| 1.20 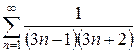
|
1.21 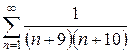
| 1.22 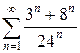
|
1.23 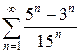
| 1.24 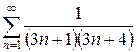
|
1.25 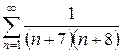
| 1.26 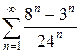
|
1.27 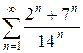
| 1.28 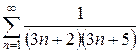
|
1.29 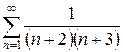
| 1.30 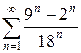
|
2.1 а) 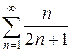 б)
б) 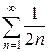 в)
в) 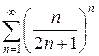
г) 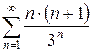 д)
д) 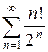 е)
е) 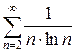
ж) 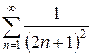 з)
з) 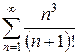 и)
и) 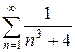
2.2 а) 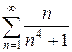 б)
б) 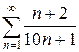 в)
в) 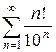
г) 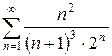 д)
д) 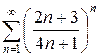 е)
е) 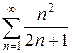
ж) 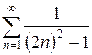 з)
з) 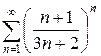 и)
и) 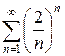
2.3 а) 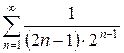 б)
б) 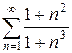 в)
в) 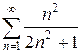
г) 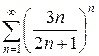 д)
д) 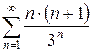 е)
е) 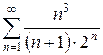
ж) 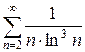 з)
з) 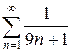 и)
и) 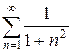
2.4 а) 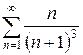 б)
б) 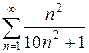 в)
в) 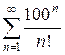
г) 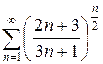 д)
д) 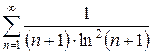 е)
е) 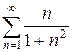
ж) 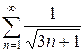 з)
з) 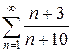 и)
и) 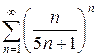
2.5 а) 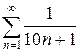 б)
б)  в)
в) 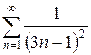
г) 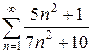 д)
д) 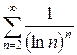 е)
е) 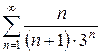
ж) 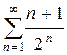 з)
з) 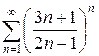 и)
и) 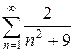
2.6 а) 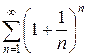 б)
б) 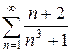 в)
в) 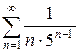
г) 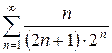 д)
д) 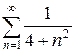
е) 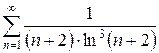 ж)
ж) 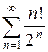 з)
з) 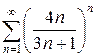 и)
и) 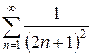
2.7 а) 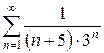 б)
б) 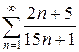 в)
в) 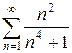
г) 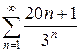 д)
д) 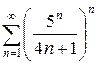 е)
е) 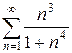
ж) 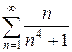 з)
з) 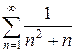 и)
и) 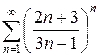
2.8 а) 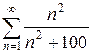 б)
б) 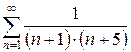 в)
в) 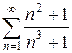
г) 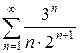 д)
д) 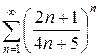
е) 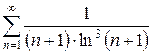 ж)
ж) 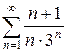 з)
з) 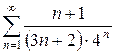 и)
и) 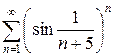
2.9 а) 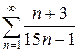 б)
б) 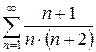 в)
в) 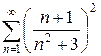
г) 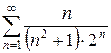 д)
д) 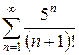 е)
е) 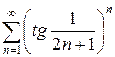
ж) 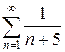 з)
з) 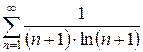 и)
и) 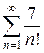
2.10 а) 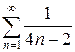 б)
б) 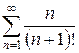 в)
в) 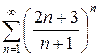
г) 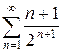 д)
д) 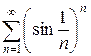 е)
е) 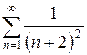
ж) 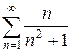 з)
з) 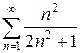 и)
и) 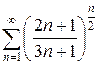
2.11 а) 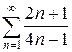 б)
б) 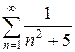 в)
в) 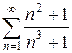
г) 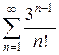 д)
д) 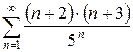 е)
е) 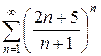
ж)  з)
з) 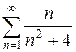
и) 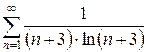
2.12 а) 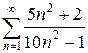 б)
б) 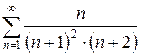 в)
в) 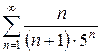
г) 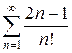 д)
д) 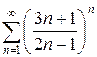 е)
е) 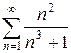
ж) 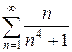 з)
з) 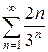 и)
и) 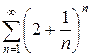
2.13 а) 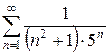 б)
б) 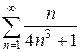 в)
в) 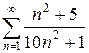
г) 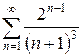 д)
д) 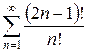 е)
е) 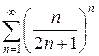
ж) 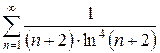 з)
з) 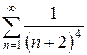 и)
и) 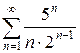
2.14 а) 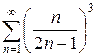 б)
б) 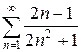 в)
в) 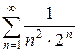
г) 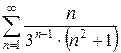 д)
д) 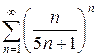 е)
е) 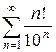
ж) 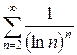 з)
з) 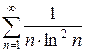 и)
и) 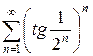
2.15 а) 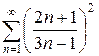 б)
б) 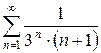 в)
в) 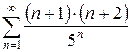 г)
г) 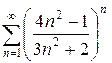 д)
д) 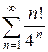 е)
е) 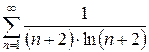 ж)
ж) 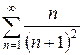 з)
з) 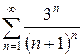
и) 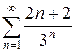
2.16 а) 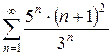 б)
б) 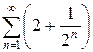 в)
в) 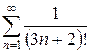
г) 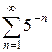 д)
д) 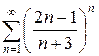 е)
е) 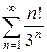
ж) 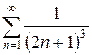 з)
з) 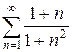 и)
и) 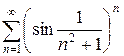
2.17 а) 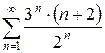 б)
б) 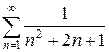 в)
в) 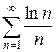
г) 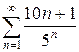 д)
д) 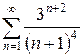 е)
е) 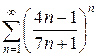
ж) 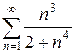 з)
з) 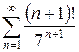 и)
и) 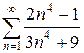
2.18 а) 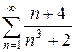 б)
б) 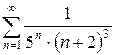 в)
в) 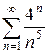
г) 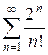 д)
д) 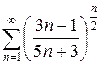 е)
е) 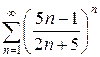
ж) 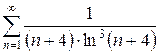 з)
з) 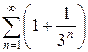 и)
и) 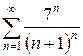
2.19 а) 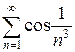 б)
б)  в)
в) 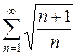
г) 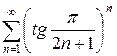 д)
д) 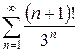 е)
е) 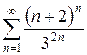
ж) 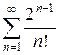 з)
з) 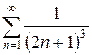
и) 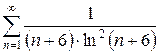
2.20 а) 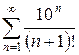 б)
б) 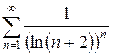 в)
в) 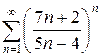
г) 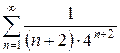 д)
д) 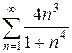 е)
е) 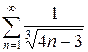
ж) 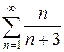 з)
з) 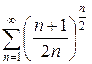 и)
и) 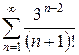
2.21 а) 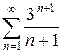 б)
б) 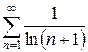 в)
в) 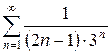
г) 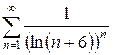 д)
д) 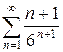 е)
е) 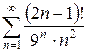
ж) 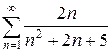 з)
з) 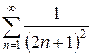 и)
и) 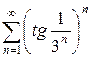
2.22 а) 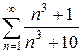 б)
б) 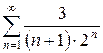 в)
в) 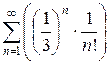
г) 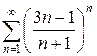 д)
д) 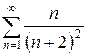 е)
е) 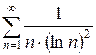
ж) 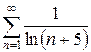 з)
з) 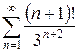 и)
и) 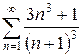
2.23 а) 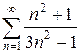 б)
б) 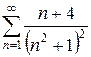 в)
в) 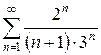
г) 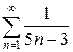 д)
д) 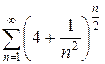 е)
е) 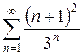
ж) 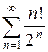 з)
з) 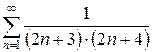 и)
и) 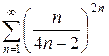
2.24 а) 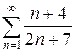 б)
б) 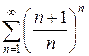 в)
в) 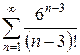
г) 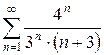 д)
д) 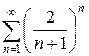 е)
е) 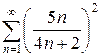
ж) 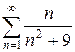 з)
з) 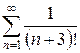 и)
и) 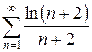
2.25 а) 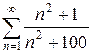 б)
б) 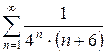 в)
в) 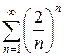
г) 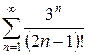 д)
д) 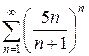 е)
е) 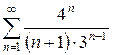
ж) 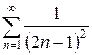 з)
з) 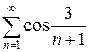 и)
и) 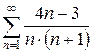
2.26 а) 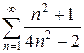 б)
б) 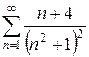 в)
в) 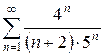
г) 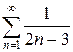 д)
д) 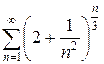 е)
е) 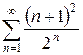
ж) 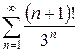 з)
з) 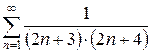 и)
и) 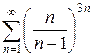
2.27 а) 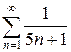 б)
б) 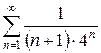 в)
в) 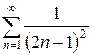
г) 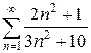 д)
д) 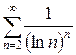 е)
е) 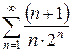
ж) 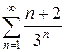 з)
з) 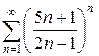 и)
и) 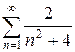
2.28 а) 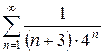 б)
б)  в)
в) 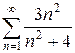
г) 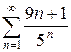 д)
д) 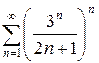 е)
е) 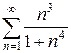
ж) 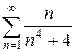 з)
з) 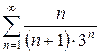 и)
и) 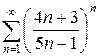
2.29 а) 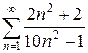 б)
б) 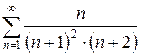 в)
в) 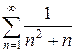
г) 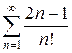 д)
д) 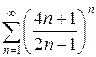 е)
е) 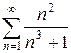
ж) 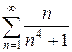 з)
з) 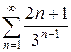 и)
и) 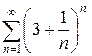
2.30 а) 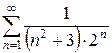 б)
б) 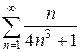 в)
в) 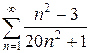
г) 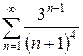 д)
д) 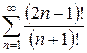 е)
е) 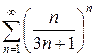
ж) 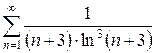 з)
з) 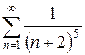 и)
и) 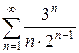
3.1 а) 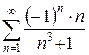 б)
б) 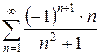
3.2 а) 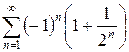 б)
б) 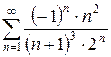
3.3 а) 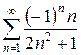 б)
б) 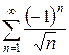
3.4 а) 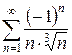 б)
б) 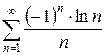
3.5 а) 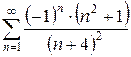 б)
б) 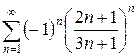
3.6 а) 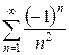 б)
б) 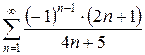
3.7 а) 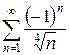 б)
б) 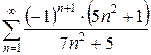
3.8 а) 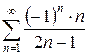 б)
б) 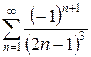
3.9 а) 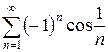 б)
б) 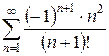
3.10 а) 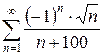 б)
б) 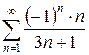
3.11 а) 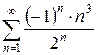 б)
б) 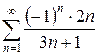
3.12 а) 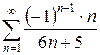 б)
б) 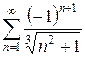
3.13 а) 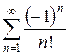 б)
б) 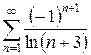
3.14 а) 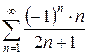 б)
б) 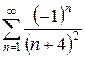
3.15 а) 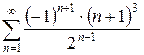 б)
б) 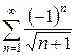
3.16 а) 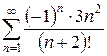 б)
б) 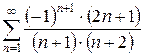
3.17 а) 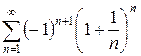 б)
б) 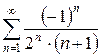
3.18 а) 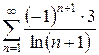 б)
б) 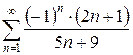
3.19 а) 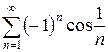 б)
б) 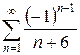
3.20 а) 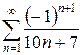 б)
б) 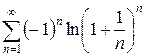
3.21 а) 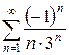 б)
б) 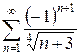
3.22 а) 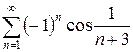 б)
б) 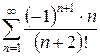
3.23 а) 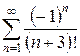 б)
б) 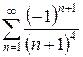
3.24 а) 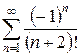 б)
б) 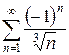
3.25 а) 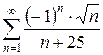 б)
б) 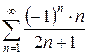
3.26 а) 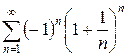 б)
б) 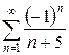
3.27 а) 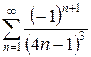 б)
б) 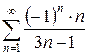
3.28 а) 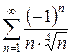 б)
б) 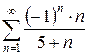
3.29 а) 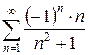 б)
б) 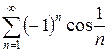
3.30 а) 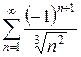 б)
б) 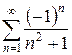
4.1 а) 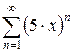 б)
б) 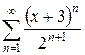
4.2 а) 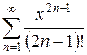 б)
б) 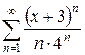
4.3 а) 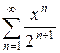 б)
б) 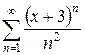
4.4 а) 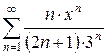 б)
б) 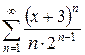
4.5 а) 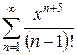 б)
б) 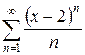
4.6 а) 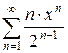 б)
б) 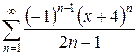
4.7 а) 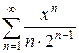 б)
б) 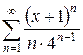
4.8 а) 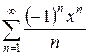 б)
б) 
4.9 а) 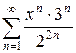 б)
б) 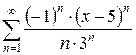
4.10 а) 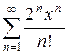 б)
б) 
4.11 а) 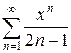 б)
б) 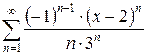
4.12 а) 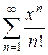 б)
б) 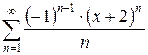
4.13 а) 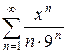 б)
б) 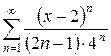
4.14 а) 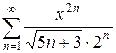 б)
б) 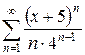
4.15 а) 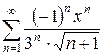 б)
б) 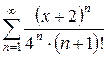
4.16 а) 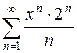 б)
б) 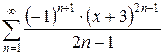
4.17 а) 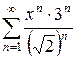 б)
б) 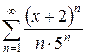
4.18 а) 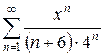 б)
б) 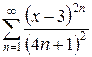
4.19 а) 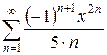 б)
б) 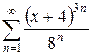
4.20 а) 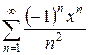 б)
б) 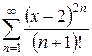
4.21 а) 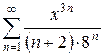 б)
б) 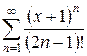
4.22 а) 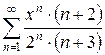 б)
б) 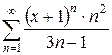
4.23 а) 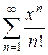 б)
б) 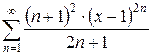
4.24 а) 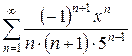 б)
б) 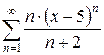
4.25 а) 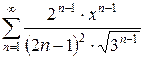 б)
б) 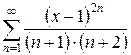
4.26 а) 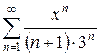 б)
б) 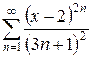
4.27 а) 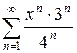 б)
б) 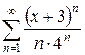
4.28 а) 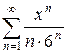 б)
б) 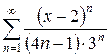
4.29 а) 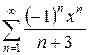 б)
б) 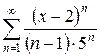
4.30 а) 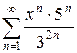 б)
б) 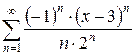
5.1 a) 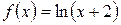
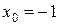 б)
б) 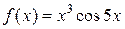
5.2 a) 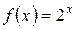
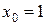 б)
б) 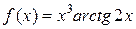
5.3 a) 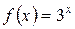
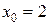 б)
б) 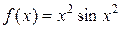
5.4 a) 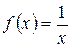
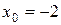 б)
б) 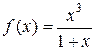
5.5 a) 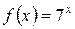
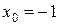 б)
б) 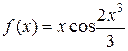
5.6 a) 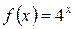
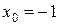 б)
б) 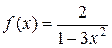
5.7 a) 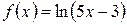
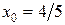 б)
б) 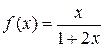
5.8 a) 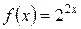
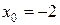 б)
б) 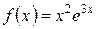
5.9 a) 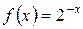
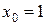 б)
б) 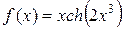
5.10 a) 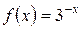
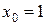 б)
б) 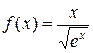
5.11 a) 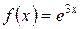
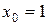 б)
б) 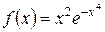
5.12 a) 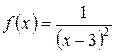
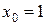 б)
б) 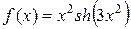
5.13 a) 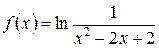
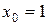 б)
б) 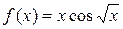
5.14 a) 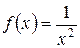
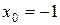 б)
б) 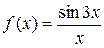
5.15 a) 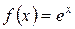
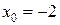 б)
б) 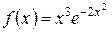
5.16 a) 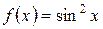
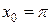 б)
б) 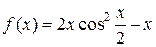
5.17 a) 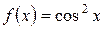
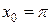 б)
б) 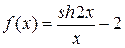
5.18 a) 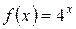
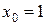 б)
б) 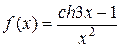
5.19 a) 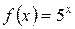
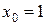 б)
б) 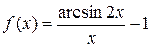
5.20 a) 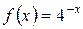
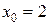 б)
б) 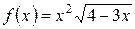
5.21 a) 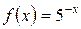
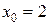 б)
б) 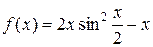
5.22 a) 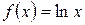
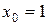 б)
б) 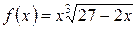
5.23 a) 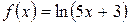
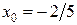 б)
б) 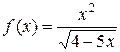
5.24 a) 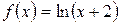
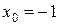 б)
б) 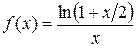
5.25 a) 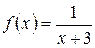
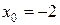 б)
б) 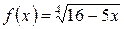
5.26 a) 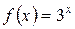
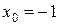 б)
б) 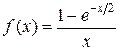
5.27 a) 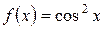
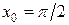 б)
б) 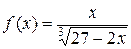
5.28 a) 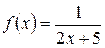
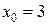 б)
б) 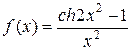
5.29 a) 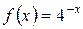
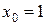 б)
б) 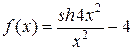
5.30 a) 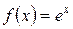
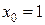 б)
б) 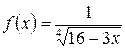
Список используемой литературы
1. Высшая математика для экономистов: учебник для студентов вузов, обучающихся по экономическим специальностям / Н. Ш. Кремер [и др.]; ред. Н. Ш. Кремер. - 3-е изд. - М: ЮНИТИ-ДАНА, 2009. - 480с. (гриф минобразования).
2. Лунгу К.Н., Норин В.П., Письменный Д.Т. Сборник задач по высшей математике. 1 курс/Под ред. С.Н. Федина. – М.: Айрис – пресс, 2004. – 576с.
3. Лунгу К.Н., Норин В.П., Письменный Д.Т. Сборник задач по высшей математике. 2 курс/Под ред. С.Н. Федина. – М.: Айрис – пресс, 2004. – 592с.
4. Общий курс высшей математики для экономистов: учебник для студентов вузов, обучающихся по экономическим специальностям / РЭА им. Г. В. Плеханова; ред. В. И. Ермаков. - М: ИНФРА-М, 2007. - 656с. (гриф минобразования).
5. Пискунов Н. С. Дифференциальное и интегральное исчисления. Т. 1.: учебное пособие для студентов втузов: в 2 т. / Н. С. Пискунов. - Изд. стер. - М: Интеграл-Пресс, 2009. - 416с.
6. Шипачев В. С. Курс высшей математики: учебник для студентов вузов / В. С. Шипачев. - 4-е изд., испр. - М: Оникс, 2009. - 600с.
 2015-01-30
2015-01-30 792
792








