| № п/п | Уравнение | Система нормальных уравнений | Графическое изображение |
Прямой
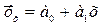 или
или
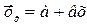 (связь прямолинейная)
(связь прямолинейная)
| 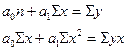
| у 0 х | |
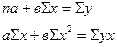
| |||
| 2 | |||
 2 2
| Парабола второго порядка
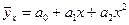 или
или
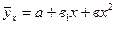 или
или
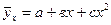 (связь криволинейная)
(связь криволинейная)
| 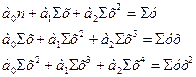
| |
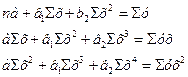
| |||
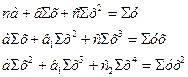
| |||
Кубическая парабола
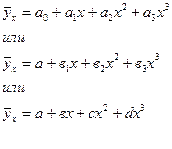 (связь криволинейная)
(связь криволинейная)
| 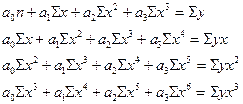
| ||
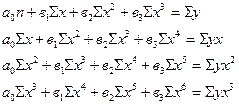
| |||
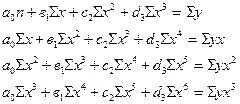
| |||
Гипербола
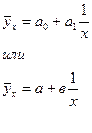 (связь криволинейная)
(связь криволинейная)
| 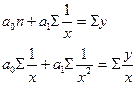
| у 0 х | |
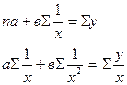
| |||
Логарифмическая кривая
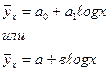 (связь криволинейная)
(связь криволинейная)
| ℓog х = k
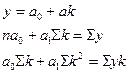
| у О х | |
| ℓog х = k у= а + вk nа + вΣk =Σу аΣk + вΣk² =Σуk |
Решая системы нормальных уравнений, определяют параметры 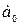 и
и 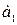 уравнения связи:
уравнения связи:
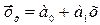
Параметры 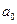 и
и 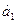 можно определить по формулам:
можно определить по формулам:
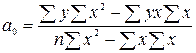 ,
,
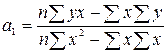 .
.
Параметр 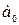 - показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов.
- показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов.
Параметр 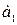 (коэффициент регрессии) показывает, насколько
(коэффициент регрессии) показывает, насколько
изменяется в среднем значение результативного признака при увеличении факторного на единицу.
На основе этого параметра (коэффициента регрессии) вычисляются коэффициенты эластичности, которые показывают изменение
результативного признака в % в зависимости от изменения факторного признака на 1 %.
Коэффициент эластичности: 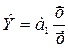 ;
;
Эмпирический (перекрестный)
коэффициент эластичности: 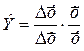 ;
;
где Э – процентные изменения результативного показателя у при изменении х;
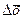 – прирост фактора х;
– прирост фактора х;
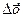 – прирост результативного показателя у;
– прирост результативного показателя у;
Основные этапы проведения корреляционного анализа показаны
на рис. 8.1.
 2015-01-30
2015-01-30 315
315








