Лекция 3 – Работа Ивана Алексеевича Вышнеградского

Работы Д.-К. Максвелла, И.А.Вышнеградского, А.Стодолы,

Заложивших основу ТАР

Лекция 3 – Работа Ивана Алексеевича Вышнеградского

«О регуляторах прямого действия» (1876)

И. А. Вышнеградский (1831—1895)

Иван Алексеевич Вышнеградский родился 20 декабря 1831 г. в городе Вышний Волочок Тверской губернии в семье священника, в 1843 г. посту­пил в Тверскую духовную семинарию, в 1846 г. переехал в Петербург и поступил на физико-математический факультет Главного педагогического института.

В 1851г. И.А. Вышне­градский окончил физико-математический факультет Главного педагогического института с серебряной медалью и со званием старшего учителя и был назначен преподавателем математики во 2-й Петербургский кадетский корпус.

С 1851 по 1854 г. И. А. Вышнеградский одновременно с преподаванием в кадетском корпусе си­стематически совершенствует свои знания в области математики и аналитической механики под руководством М. В. Остроградского. Он успешно сдает магистерские экзаме­ны и в 1854 г. защищает в Санкт-Петербургском университете диссер­тацию на степень магистра математических наук: «О движении системы материальных точек, определяемой полными диффе­ренциальными уравнениями». Официальными оппонентами при защите диссертации были П. Л. Чебышев и О. И. Сомов.

В 1854 г. И.А.Вышнеградский по рекомен­дации М.В.Остроградского получил место преподавателя мате­матики в Михайловском артиллерийском училище, которое в последующем (с 1855 года) преобразовывается в высшее учебное заве­дение - Михайловскую артиллерийскую академию. Преподавательская деятельность в артиллерийских учебных заведениях, общение с артиллеристами и военными ин­женерами, Крымская война, обнаружившая необходимость модернизации стрелкового оружия и артиллерии, оказали существенное влияние на на­правление научных интересов И. А. Вышнеградского.

В 1858 г. ему поручают чтение лекций по прикладной механике, и в том же году он командируется Академией в Киев, Шостку и Брянск для детального ознакомления с заводами артиллерийского ведомства. С этого времени деятельность И. А. Вышнеградского получает отчетливое прикладное на­правление. Он преподает различные отделы прикладной механи­ки, ведет курсы проектирование механизмов и выступает как конструктор и инженер-практик.

В 1859 г. Михайловская артиллерийская академия предоставляет И. А. Вышнеградскому длительную заграничную командировку для подготовки к званию профессора «практической механики». К своему отъезду за границу И. А. Вышнеградский уже имел ряд опубликованных научных работ и серьезный практический инженерный опыт.

И. А. Вышнеградский начал свою заграничную команди­ровку с Гейдельберга, где он слушал лекции по теоретической и экспериментальной физике у знаменитого Кирхгофа и лекции по математике у Гессе и Кенигсбергера. Затем он провел около года в Политехническом институте города Карлсруэ, где тогда работал один из основоположников научного машиностроения Редтенбахер, виднейший математик и специалист в области теории упругости Клебш.

По возвращении в 1862 г. в Россию И. А. Вышнеградский был утвержден профессором практической механики Михай­ловской артиллерийской академии, а вскоре и профессором механики Санкт-Петербургского технологического института.

В обоих этих учебных заведениях он развернул интен­сивную профессорскую деятельность. Он читал различные курсы по машиностроению и машиноведению и по смежным научным дисциплинам, а также вел курсовое и дипломное проектирование. Он воспитал целое поколение русских инженеров-машино­строителей, был главой первой русской школы в области машиностроения.

Работы по регулированию, которые прославили его имя, были опубликованы в 1877—1878 гг. в «Известиях Технологического Института» - издании, которое было основано самим И.А.Вышнеградским для печатания работ по различным приложениям науки и техники. Наиболее важной из них явилась работа «О регуляторах прямого действия» (1876), давшая ответ на жизненно важные вопросы практики регуляторостроения и устойчивости паровых машин.

Фрагмент первого издания работы «О регуляторах прямого действия»

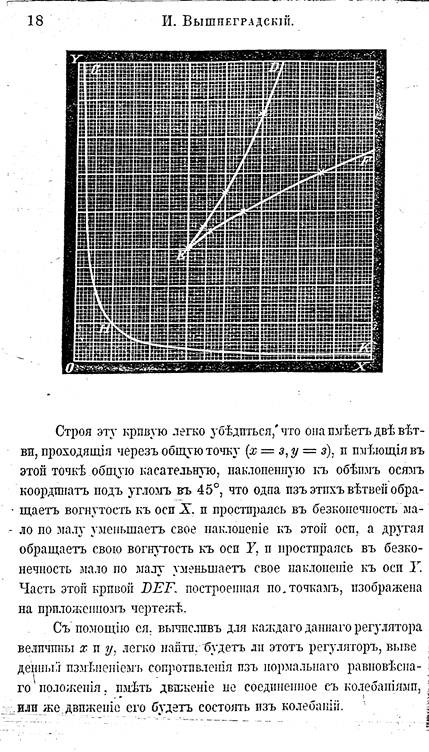
В своей работе «О регуляторах прямого действия» (1876), Вышнеградский применил тот же математический прием описания динамики, что и Максвелл - заменил все сложные зависимости между определяющими поведение системы переменными простой пропорциональностью. В отличие от Максвелла он не стал учитывать при описании динамики свойство (ввиду его незначительности) паровой машины к саморегулированию (принял 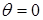), а за регулирующее устройство принял статический регулятор Уатта (условная принципиальная схема регулирования частоты вращения с помощью регулятора Уатта представлена на рисунке 3.1).

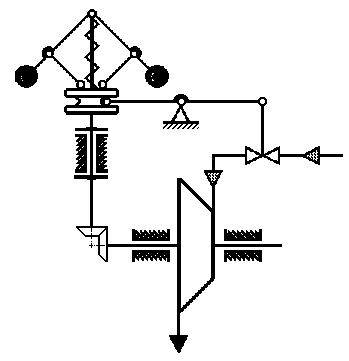
Рисунок 3.1 - Условная схема регулирования частоты вращения

паровой машины с помощью регулятора Уатта

В результате Вышнеградский пришел к следующим уравнениям, описывающим динамику системы автоматического регулирования «машина-статический регулятор»:

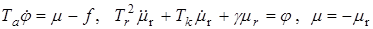. (3.1)

Здесь также первое уравнение определяет динамику машины-двигателя (без саморегулируемости), второе - динамику статического регулятора.

В описании (3.1) значение положительного коэффициента 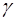соответствует статической погрешности регулятора (характеризует меру неспособности регулятора поддерживать частоту вращения идеально постоянной во всем диапазоне изменения нагрузки). В дальнейшем коэффициент стали называть коэффициентом неравномерности (для астатического регулятора ).

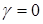Структурная модель системы (3.1) представлена на рисунке 3.2.

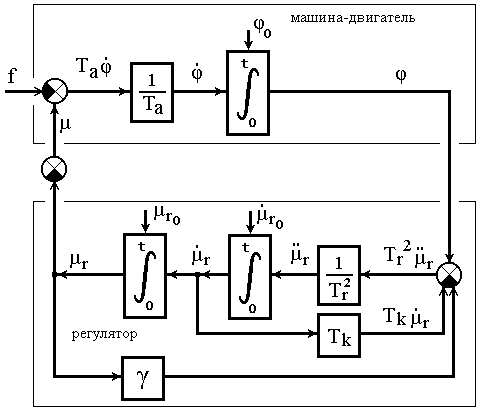
Рисунок 3.2 - Структурная математическая модель системы:

машина-двигатель, управляемая статическим регулятором

При совместном решении уравнений (3.1) относительно 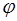или 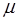динамика (движения) системы автоматического регулирования «машина-статический регулятор» описывается линейным дифференциальным уравнением третьего порядка:

а) относительно переменной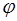

(3.2)

б) относительно переменной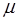

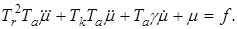(3.3)

В структурном виде описание (3.3) представлено на рисунке 3.3.

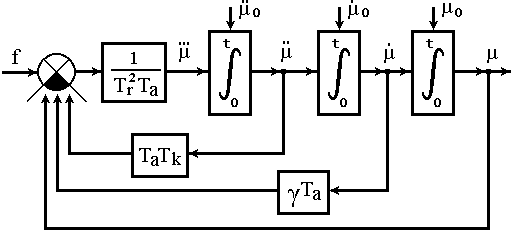
Рисунок 3.3 - Структурная математическая модель системы:

машина-двигатель, управляемая статическим регулятором

Одно уравнение состояний равновесия системы автоматического регулирования можно получить из (3.2) при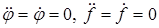

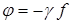, (3.4)

второе уравнение состояний равновесия системы автоматического регулирования можно получить из (3.3) при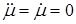

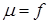. (3.5)

Характеристическое уравнение системы определяется выражением:

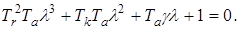(3.6)

За условие устойчивости состояний равновесия (также, как и в работе Максвелла) было принято условие отрицательности корней (отрицательности вещественных частей корней) уравнения (3.6). Таким условием стало неравенство

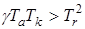. (3.7)

Полученное условие (3.7) легко объяснило причину «бунта» машин. Ведь совершенствование паровых машин, повышение их мощности и числа оборотов сопровождалось облегчением маховика (уменьшением коэффициента 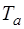), желание повысить точность (приблизить работу статического регулятора к астатическому) сопровождалось уменьшением неравномерности (уменьшением коэффициента 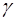) и, как следствие, к увеличению массы подвижных частей регулятора (увеличению коэффициента 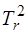). Оставался последний коэффициент (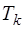), с помощью которого можно было выполнить неравенство (3.7), однако для этого требовалось применение катаракта - особого устройства, порождающего вязкое трение в регуляторе (увеличение коэффициента ).

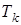Анализируя полученное им неравенство, Вышнеградский сформулировал свои знаменитые тезисы:

1) без неравномерности (коэффициент 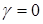) нет регулятора;

2) без катаракта (коэффициент ) нет регулятора.

Формулировка первого тезиса соответствовала тому, что астатический регулятор (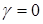) непригоден для регулирования машин, лишенных свойства саморегулируемости (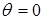). Второй тезис означал, что всякий чувствительный (сухое трение отсутствует) регулятор обязательно должен иметь катаракт - устройство, обеспечивающее (представлено на рисунке 3.3).

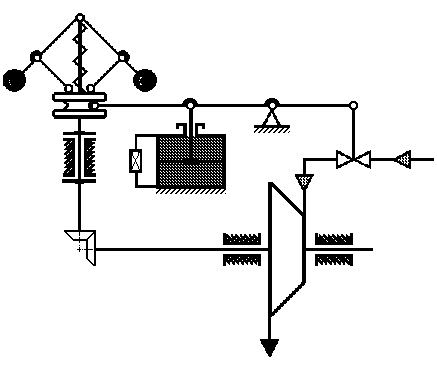
Рисунок 3.4 – Условная схема регулирования частоты вращения паровой машины

регулятором Уатта, снабженным дополнительным устройством - катарактом

Сравнение результатов, полученных Максвеллом и Вышнеградским. Как уже говорилось, к середине XIX века, в связи с ростом мощности и быстроходности паровых машин, все чаще стала про­являться склонность машин к неустойчивой paботе (самораскачиванию). Статические, центробежные регуляторы Уатта, уверенно обеспечивающие надежную работу машин меньшей мощности, оказались для мощных машин по непонятным причинам малопригодными.

Статья Максвелла «О регуляторах» стала первой успешной попыткой математического осмысления работы системы «машина-регулятор». Впервые теоретически была исследована, с позиций динамики, работа машины-двигателя, снабженной регулятором частоты вращения, и выяснены причины возникновения неустойчивости. За условие устойчивости системы было принято условие отрицательности корней (отрицательности вещественных частей корней) характеристического уравнения 3-го порядка.

Однако, рекомендация Максвелла использовать для регулирования частоты вращения астатические регуляторы (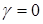) требовала наличия у машины-двигателя существенного свойства к саморегулированию (). Поскольку в рассматриваемый период основным двигателем являлась паровая машина, свойство саморегулирования у которой выражено очень слабо (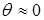), выводы работы не получили практического применения.

И.А.Вышнеградский подошел к делу иначе - не только как математик, а в большей степени как инженер-практик. Свои работы он посвятил насущной проблеме – регулированию паровой машины, снабженной статическим регулятором Уатта.

Полученная Вышнеградским компактная формула (3.7), показала, почему регуляторы Уатта перестали надежно работать. Машины, которые строил сам Уатт, были машинами низкого давления, маломощными, с большими маховиками (существенное значение коэффициента ), обеспечивающим плавное вращение тихоходных машин того времени, а регуляторы работали с неравномерностью (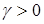), т.е. число оборотов при различной нагрузке на машину было различным. Это обеспечивало устойчивую ра­боту машин (условие 3.7).

Развитие техники выдвинуло повышенные требования к точ­ности регулирования, для чего пришлось уменьшать коэффициент неравномерности регулятора (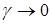). Увеличение быстроходности машин делало ненужным использование дополнительного маховика (уменьшение коэффициента ), а увеличение мощности машин потребовало больших усилий для перемещения заслонки, что требовало увеличения массы грузов регулятора (увеличение коэффициента 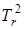). Все это с неизбеж­ностью вело к неустойчивости (смотри условие 3.7). Лишь после того, как это обстоя­тельство было выяснено Вышнеградским, стало возможно целенаправленно бороться с неустойчивостью (самораскачиванием).

Вышнеградский первым дает наглядную геометрическую интерпретацию полученных условий устойчивости (3.7) - отрицательности корней характеристического уравнения (3.6). Для придания наглядности своим выводам (сокращения числа коэффициентов в левых частях уравнений (3.2), (3.3) Вышнеградский использует оригинальный способ приведения коэффициента при старшей производной в уравнениях (3.2), (3.3) к единице.

Так, например, взяв первое слагаемое в уравнении (3.3) и применив несложные преобразования

,

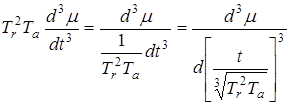можно реальное время 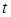заменить на другое (безразмерное) время 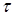. При этом реальное время 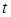с «новым» временем 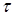будут связаны зависимостью .

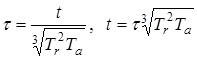Примечание. Такой прием называется массштабированием времени, используется для сокращения числа коэффициентов в уравнениях динамики.

Заменив в левой части, например, уравнения (3.3) реальное время 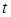на «новое» время 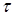, можно получить (при 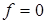) следующее уравнение динамики (уравнение свободных движений в системе).

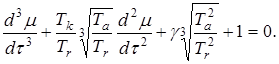(3.8)

Обозначив соответственно и 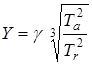получим характеристическое уравнение (3.7) в следующем виде

, (3.9)

где - обобщенные безразмерные положительные параметры (получившие впоследствии название параметров Вышнеградского).

При новых параметрах условие устойчивости (3.7) принимает вид

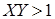. (3.10)

а уравнение 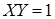(названное впоследствии гиперболой Вышнеградского) отделяет на плоскости параметров 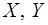область значений параметров, соответствующих устойчивой работе системы от области, где имеет место неустойчивость (представлено на рисунке 3.5, где гипербола обозначена буквами GHK).

Анализируя формулу Кардано, Вышнеградский идет дальше, чем получение условий устойчивости и решает уже вопрос качества регулирования, получая внутри области устойчивости области различного качества регулирования.

Примечание. ИмяИеронима Кардано (Geloramo Cardano, 1501 - 1576) связано с другим именем итальянского математика Сципиона (Тарталья), который с 1535 года владел умением находить корни кубического уравнения, но метод нахождения корней держал в тайне. Наконец, он раскрыл свой метод И.Кордано, но взял с него клятву сохранить метод в тайне. В 1545 г. Кардано опубликовал под своим именем книгу по алгебре «Великое искусство», в которой (с должным признанием заслуг автора метода - Тартальи) был описан метод нахождения корней кубического уравнения. В результате судебных разбирательств и публичных взаимных оскорблений метод получил широкое распространение и известен в настоящее время как метод Кардано (формула Кардано). Защищавший Кардано на суде молодой математик Людовико Феррари впоследствии на основе метода Кардано нашел метод нахождения корней для уравнения 4-й степени, известный в настоящее время как метод Феррари (формула Феррари).

Внутри области 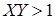Вышнеградский определяет область вещественности всех трех корней (наилучшее качество регулирования).

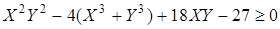. (3.11)

Область, соответствующая (3.11) ограничена линией DEF (представлено на рисунке 3.5).

В следующей своей работе, опубликованной на немецком языке, Вышнеградский дополнил свои исследования в области устойчивости, разделив ее граничной линией

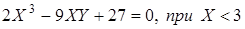(3.11)

на две подобласти (рисунок 3.5) – подобласть с малой колебательностью (область, ограниченная кривой GED и соответствует расположению корней, когда вещественный корень по отношению к паре комплексно сопряженных корней находится ближе к оси) и подобласть с существенной колебательностью (область, ограниченная кривой GEF и гиперболой GHK соотвествует расположению корней, когда пара комплексно сопряженных корней по отношению к вещественному корню находится ближе к оси).

Как видим и Максвелл и Вышнеградский вопрос об устойчивости паровой машины с регулятором свели к решению кубического алгебраического уравне­ния третьей степени, для решения которого формула - формула Кардано (Gerolamo Cordano, 1501 - 1576) - была известна еще в начале 16-го века.

Однако только Вышнеградский на основе этой формулы добился за­мечательных результатов, дав им наглядную геометрическую интерпретацию в виде, известной теперь всему миру диаг­раммы, носящей его имя.

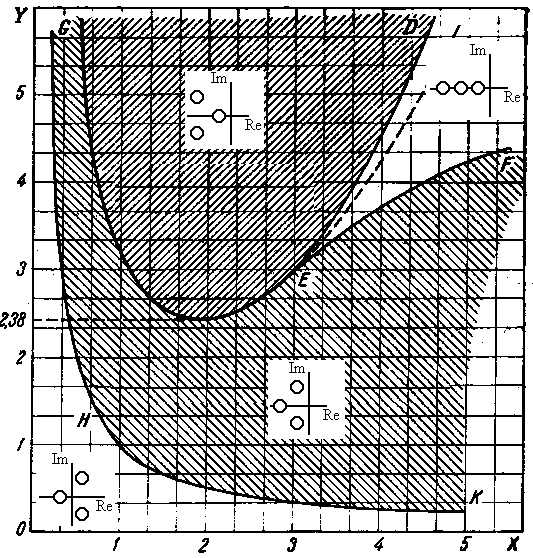
Рисунок 3.5 - Диаграмма И.А.Вышнеградского