2015-01-30
1235
Приращение плотности энергии магнитного поля равно:
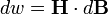
где:
H — напряжённость магнитного поля,
B — магнитная индукция
В линейном тензорном приближении магнитная проницаемость есть тензор - обозначим его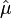 
и умножение вектора на неё есть тензорное (матричное) умножение:
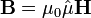
или в компонентах
.
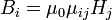Плотность энергии в этом приближении равна:
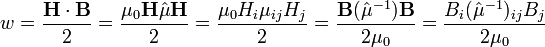
где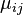 
— компоненты тензора магнитной проницаемости, 
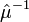— тензор, представимый матрицей, обратной матрице тензора магнитной проницаемости, 
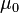— магнитная постоянная. При выборе осей координат совпадающими с главными осями[13] тензора магнитной проницаемости формулы в компонентах упрощаются:
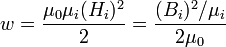
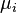— диагональные компоненты тензора магнитной проницаемости в его собственных осях (остальные компоненты в данных специальных координатах — и только в них! — равны нулю). В изотропном линейном магнетике:
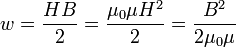
где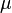 
— относительная магнитная проницаемость. В вакууме
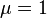
и
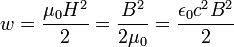
Энергию магнитного поля в катушке индуктивности можно найти по формуле:
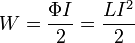
где Ф — магнитный поток, I — ток, L — индуктивность катушки или витка с током.
