Прочитайте предложенные рассуждения и примеры. Ответьте письменно на вопросы и решите задачи.
Определение производной функции, ее геометрический и физический смысл, ее свойства подробно описаны в §13 лекций. Займемся непосредственно вычислением производных, для чего используем сводную таблицу формул дифференцирования. Вторая часть таблицы, в которой приведены производные основных элементарных функций, записана для сложных функций вида f (u), u = u (x). При этом следует помнить, что 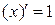 .
.
Примеры.
Вычислить производные функций:
а) 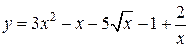 ; б)
; б) 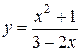 ; в)
; в) 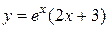 ; г)y= sin 2x; д)y= ln(x2+ 1)
; г)y= sin 2x; д)y= ln(x2+ 1)
Решение:
а) 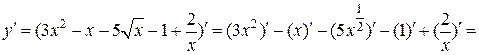
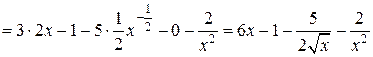 .
.
б) 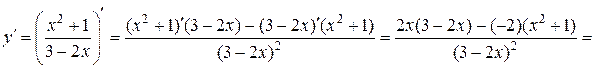
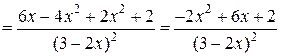 .
.
в) 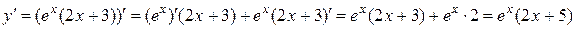 .
.
г) 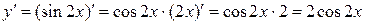 .
.
д) 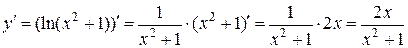 .
.
Производная широко применяется в исследовании функции и при решении связанных с этим практических задач.
В том числе дифференцирование применяют для вычисления пределов, используя так называемое правило Лопиталя:
Предел отношения функций, представляющий неопределенность вида 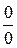 или
или 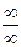 , равен пределу отношения их производных:
, равен пределу отношения их производных: 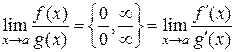
 2015-01-30
2015-01-30 287
287








