2015-01-30
425
Рассмотрим случай, когда материальная точка движется из точки 1 в точку 2 под действием приложенных к ней сил (рис.4.4.)
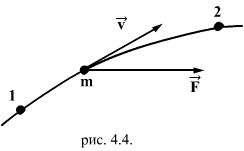
Причем силы, действующие на материальную точку, могут иметь разную природу, т.е. могут быть консервативными и неконсервативными. Уравнение движения в этом случае запишется в виде
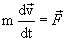
| (4.6) |
где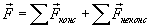 
Перепишем (4.6) в виде
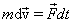
| (4.7) |
Умножим скалярно уравнение (4.7) на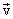 
и проинтегрируем от точки1 до точки 2, получим:
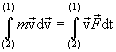
| (4.8) |
Учитываем то, что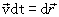 
, и интеграл в правой части выражения (4.8) представляет собой работу всех сил, на участке 1-2, можно записать:
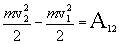
| (4.9) |
величина
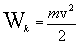
| (4.10) |
называется кинетической энергией материальной точки. Таким образом, кинетическая энергия материальной точки – это энергия, которой обладает эта точка вследствие своего движения.
Из полученного выражения (4.9) следует, что работа всех сил, действующих на материальную точку на участке траектории 1-2 равна изменению ее кинетической энергии на этом участке.
