Кинетическая энергия вращающегося твердого тела

Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:

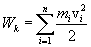
Если тело вращается вокруг неподвижной оси с угловой скоростью 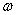, то линейная скорость i-ой точки равна 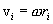, где 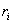, - расстояние от этой точки до оси вращения. Следовательно.

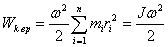
где 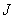- момент инерции тела относительно оси вращения.

В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости 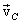центра инерции тела, и вращения с угловой скоростью 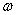вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду

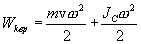
где 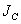- момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.