Формула полной вероятности и теорема гипотез (формула Бейеса)

Пусть необходимо найти вероятность P(A) события A, которое обязательно произойдет с одним из событий 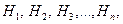образующих полную группу несовместных событий.

В этом случае P(A) называется полной вероятностью, а события 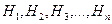- гипотезами.

Полная вероятность находится по формуле:

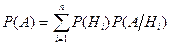, (7)

где 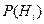- вероятность i -той гипотезы,

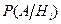- вероятность события A при условии, что произошла гипотеза 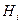(условная вероятность). .

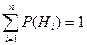Теорема гипотез (формула Бейеса).

Если для несовместных гипотез 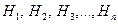известны априорные (до опыта) вероятности 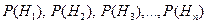и условные вероятности события A, то после осуществления события A апостериорные (после опыта) вероятности гипотез найдутся по формуле Бейеса:

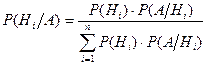. (8)

При решении задач необходимо:

1) определить пространство событий данной задачи, то есть обозначить искомое событие A, гипотезы 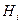и условные события ;

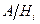2) вычислить вероятности гипотез 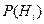и условные вероятности 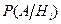, если они не заданы. Если же вероятности заданы, то выяснить, какие из заданных вероятностей относятся к условным вероятностям, а какие - к вероятностям гипотез, учитывая, что ;

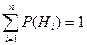3) посчитать искомую вероятность P(A) по формуле (7);

4) если событие A произошло, то условные вероятности гипотез (апостериорные) посчитать по формуле (8).

Пример решения.Задача 1.

Пример. На трех станках-автоматах цеха обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 5% брака, второй – 7%, третий – 10%.

Производительность первого станка 15 деталей, второго – 20, третьего – 25.

а) Какова вероятность брака на выходе конвейера?

б) Каковы доли деталей каждого станка среди бракованных деталей на конвейере?