Решение. а) A – событие, состоящее в том, на выходе конвейера деталь бракованная

а) A – событие, состоящее в том, на выходе конвейера деталь бракованная.

Требуется найти вероятность P(A) – вероятность появления на выходе конвейера бракованной детали.

Система гипотез:

H₁ – гипотеза, состоящая в том, что бракованная деталь изготовлена на первом станке.

H₂ – гипотеза, состоящая в том, что бракованная деталь изготовлена на втором станке.

H₃ – гипотеза, состоящая в том, что бракованная деталь изготовлена на третьем станке.

Вероятность первой гипотезы, будет равняться отношению деталей, изготовленных на первом станка ко всем изготовленным и поступившем на конвейер деталям:

.

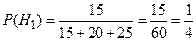Аналогично рассуждая, вероятность второй гипотезы .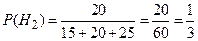

Вероятность третьей гипотезы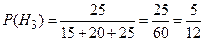

Проверка правильности составления системы гипотез:

.

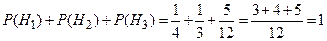Условные вероятности события A для каждой гипотезы

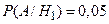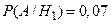(5%), (7%), 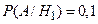(10%),

Полная вероятность события A равна

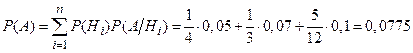
Другими словами, в массе деталей, сходящих с конвейера, брак составляет 7,75%.

б) Пусть известно, что взятая наудачу деталь – бракованная. Пользуясь формулой Байеса, найдем условные вероятности гипотез:

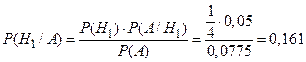
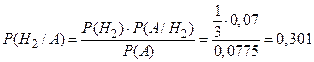
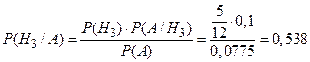
Таким образом, в общей массе бракованных деталей на конвейере доля первого станка составляет 16,1%, второго – 30,1%, третьего – 53,8%.

Задача 2. Тема: Законы распределения и числовые характеристики непрерывных случайных величин.

Функцией распределения вероятностей F(x) случайной величины X называется функция вещественной переменной x, равная вероятности того, что случайная величина X примет в результате опыта значение, меньше x.

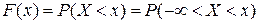
Основные свойства функция распределения .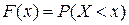

1.

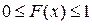
2. 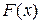– неубывающая функция, если 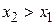, то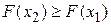

3. Для непрерывной случайной величины

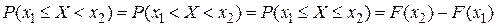
4. .

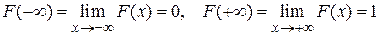Плотностью вероятности или дифференциальным законом распределения непрерывной случайной величины X называется функция f(x) вещественной переменной x, определяемая равенством

.

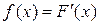Основные свойства плотности распределения f(x)

1. ;

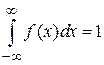2. ;

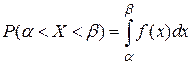4. 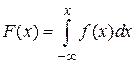- интегральный закон распределения;