| Найти | |||
| 1. | 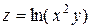
| 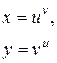
| 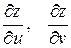
|
| 2. | 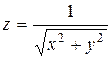
| 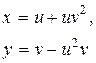
| 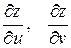
|
| 3. | 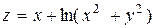
| 
| 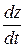
|
| 4. | 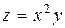
| 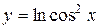
| 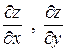 , , 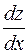
|
| 5. | 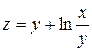
| 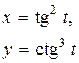
| 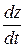
|
| 6. | 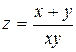
| 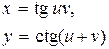
| 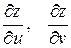
|
| 7. | 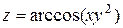
| 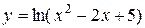
| 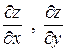 , , 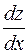
|
| 8. | 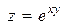
| 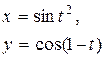
| 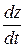
|
| 9. | 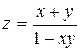
| 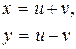
| 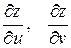
|
| 10. | 
| 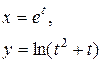
| 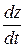
|
| 11. | 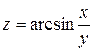
| 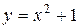
| 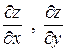 , , 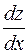
|
| 12. | 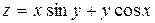
| 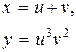
| 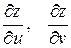
|
| 13. | 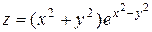
| 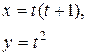
| 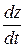
|
| 14. | 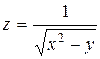
| 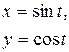
| 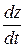
|
| 15. | 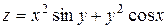
| 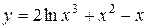
| 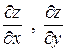 , , 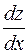
|
| 16. | 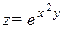
| 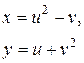
| 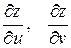
|
| 17. | 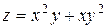
| 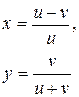
| 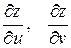
|
| 18. | 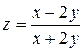
| 
| 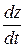
|
| 19. | 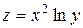
| 
| 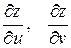
|
| 20. | 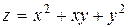
| 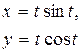
| 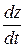
|
| 21. | 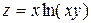
| 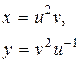
| 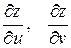
|
| 22. | 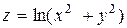
| 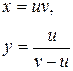
| 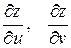
|
| 23. | 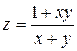
| 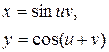
| 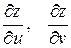
|
| 24. | 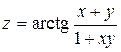
| 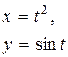
| 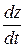
|
| 25. | 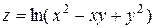
| 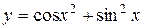
| 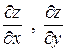 , , 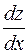
|
| 26. | 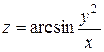
| 
| 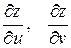
|
| 27. | 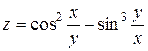
| 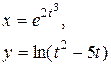
| 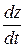
|
| 28. | 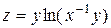
| 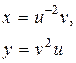
| 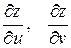
|
| 29. | 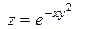
| 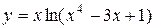
| 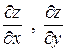 , , 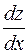
|
| 30. | 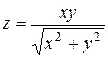
| 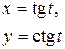
| 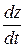
|
4. Вычислить градиент и производную функции 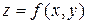 по направлению вектора
по направлению вектора 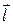 в точке
в точке 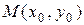 .
.
| Уравнение, задающее функцию и поверхность | Точка 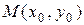
| Вектор 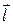
| |
| 1. | 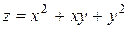
| M(1,1) | 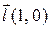
|
| 2. | 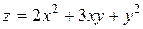
| M(2,1) | 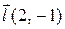
|
| 3. | 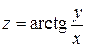
| 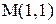
| 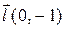
|
| 4. | 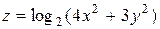
| M(1,2) | 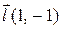
|
| 5. | 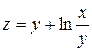
| M(1,1) | 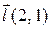
|
| 6. | 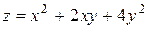
| M(2,2) | 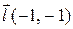
|
| 7. | 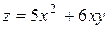
| M(2,1) | 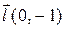
|
| 8. | 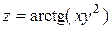
| M(2,3) | 
|
| 9. | 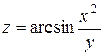
| M(1,2) | 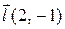
|
| 10. | 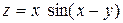
| M(1,1) | 
|
| 11. | 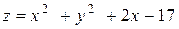
| M(2,1) | 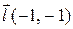
|
| 12. | 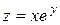
| M(2,2) | 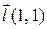
|
| 13. | 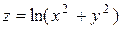
| M(3,3) | 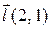
|
| 14. | 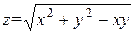
| M(2,2) | 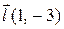
|
| 15. | 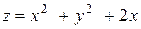
| M(3,–2) | 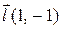
|
| 16. | 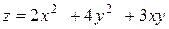
| M(2,3) | 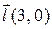
|
| 17. | 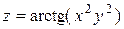
| M(2,-1) | 
|
| 18. | 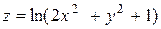
| M(2,–1) | 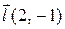
|
| 19. | 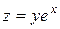
| M(1,2) | 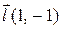
|
| 20. | 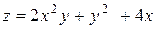
| M(3,–2) | 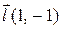
|
| 21. | 
| M(1,–2) | 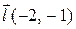
|
| 22. | 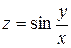
| M 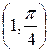
| 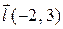
|
| 23. | 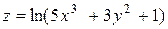
| M(1,–1) | 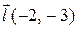
|
| 24. | 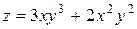
| M(1,–3) | 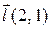
|
| 25. | 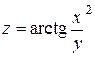
| M(1,1) | 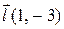
|
| 26. | 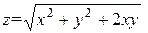
| M(2,2) | 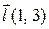
|
| 27. | 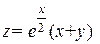
| M(0,1) | 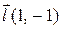
|
| 28. | 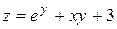
| M(5,0) | 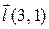
|
| 29. | 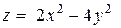
| M(2,1) | 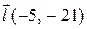
|
| 30. | 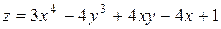
| M(1,1) | 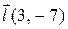
|
5. Исследовать функцию 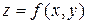 на экстремум
на экстремум
| 1. | 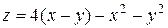
| 2. | 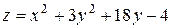
|
| 3. | 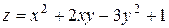
| 4. | 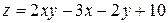
|
| 5. | 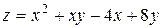
| 6. | 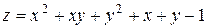
|
| 7. | 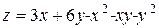
| 8. | 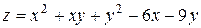
|
| 9. | 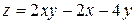
| 10. | 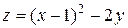
|
| 11. | 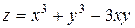
| 12. | 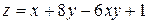
|
| 13. | 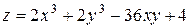
| 14. | 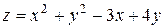
|
| 15. | 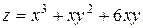
| 16. | 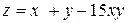
|
| 17. | 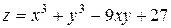
| 18. | 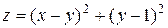
|
| 19. | 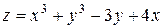
| 20. | 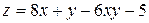
|
| 21. | 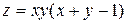
| 22. | 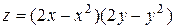
|
| 23. | 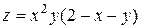
| 24. | 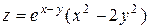
|
| 25. | 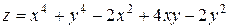
| 26. | 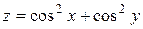
|
| 27. | 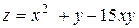
| 28. | 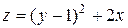
|
| 29. | 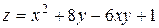
| 30. | 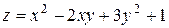
|
Исследовать функцию на условный экстремум при данных уравнениях связи
| Функция | Условие связи | ||
| 1. | 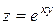
| 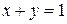
| |
| 2. | 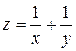
| 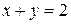
| |
| 3. | 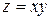
| 
| |
| 4. | 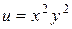
| 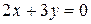
| |
| 5. | 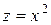
| 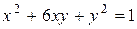
| |
| 6. | 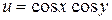
| 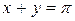
| |
| 7. | 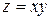
| 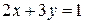
| |
| 8. | 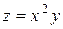
| 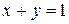
| |
| 9. | 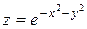
| 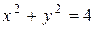
| |
| 10. | 
| 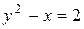
| |
| 11. | 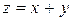
| 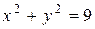
| |
| 12. | 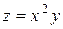
| 
| |
| 13. | 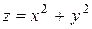
| 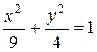
| |
| 14. | 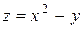
| 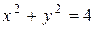
| |
| 15. | 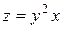
| 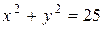
| |
| 16. | 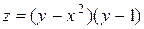
| 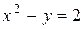
| |
| 17. | 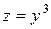
| 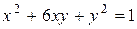
| |
| 18. | 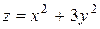
| 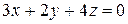
| |
| 19. | 
| 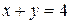
| |
| 20. | 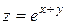
| 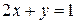
| |
| 21. | 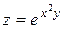
| 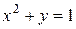
| |
| 22. | 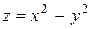
| 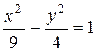
| |
| 23. | 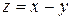
| 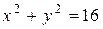
| |
| 24. | 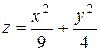
| 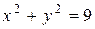
| |
| 25. | 
| 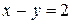
| |
| 26. | 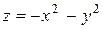
| 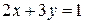
| |
| 27. | 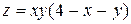
| 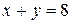
| |
| 28. | 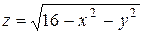
| 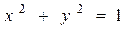 
| |
| 29. | 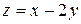
| 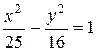
| |
| 30. | 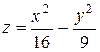
| 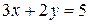
|
 2015-01-30
2015-01-30 318
318







