Пример схемы испытаний Бернулли на конкретном примере

В травматологическом отделении имеется 3 аппарата для осуществления искусственного дыхания при шоке. Больных в состоянии шока доставляют в больницу в среднем 2 раза в течение некоторого периода времени t. Вероятность отказа каждого аппарата в течение этого периода времени составляет P = 0,1. Требуется найти вероятность наступления события А, которое заключается в том, что в течение периода времени t из трех имеющихся аппаратов два будут исправны.

Обозначим через U₁ U₂ и U₃ события, состоящие в исправности первого, второго и третьего аппарата; через 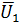, 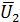и 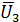— противоположные события, состоящие в неисправности (отказе в течение времени t) первого, второго и третьего аппарата. По условию задачи вероятности этих событий равны между собой.

P(U₁) = P(U₂) = P(U₃) = 1 – P = 0,9

Р( 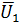) = Р( 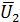) = Р( 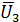) = P = 0,1

Интересующее нас событие может осуществиться тремя способами:

— исправны первый и второй аппараты, неисправен — третий (событие B₁);

— исправны первый и третий аппараты, неисправен — второй (событие В₂);

— исправны второй и третий аппараты, неисправен — первый (событие В₃).

Эти три события являются несовместными, а элементарные события, их составляющие, — независимыми. В этой задаче мы имеем дело со схемой испытаний Бернулли. Рассматриваемые события независимы (вероятность отказа каждого из аппаратов не зависит от того, что произошло с другими двумя). Условия испытаний (функционирование аппаратов в течение времени t) остаются неизменными, так как остаются неизменными вероятности отказа каждого из них. В испытании возможны только 2 исхода: отказ или безотказная работа на протяжении времени t.

Итак, нам нужно определить вероятность появления какого-либо из трех сложных несовместимых событий, каждое из которых заключается в совместном появлении трех элементарных независимых событий. Искомая вероятность может быть определена по теоремам сложения и умножения вероятностей:

Р(В₁) = P(U₁) х P(U₂) х P( )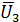

Р(В₂) = P(U₁) х P( 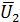) х P(U₃)

Р(В₃) = P( 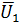) х P(U₂) х P(U₃)

Р(А) = Р(В₁) + Р(В₂) + Р(В₃) = Р (1-Р)² + Р (1-Р)² + Р (1-Р)² = 3Р (1-Р)²

Обозначим q=1-Р, тогда получим Р(А) = 3Рq²

Коэффициент «3» представляет собой число способов, которыми можно получить интересующее нас событие.

Учитывая, что Р=0,1 а q=0,9, получим значение искомой вероятности:

Р(А) = 3 х 0,1 х 0,9² = 0,243

1. Вопросы по теме занятия:

1. Значение клинической эпидемиологии и медицинской статистики для доказательной медицины.

2. Понятия вероятности, эксперимента, события, выборочного пространства (полной группы событий) в теории вероятности.

3. Достоверное и невозможное события.

4. Совместные и несовместные события. Понятие противоположных событий.

5. Понятия и примеры зависимых и независимых событий.

6. Равновозможные события. Понятие схемы случаев.

7. Классическая, эмпирическая и субъективная вероятности. Примеры, методы расчета.

8. Закон больших чисел.

9. Понятия суммы и произведения событий. Случаи их использования.

10. Основные теоремы теории вероятности.

11. Понятия априорной и апостериорной вероятностей.

12. Формула Байеса.

13. Схема испытаний Бернулли.