Рассмотрим линейную краевую задачу
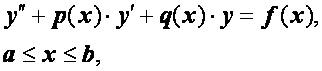 (2.24)
(2.24)
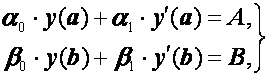 (2.25)
(2.25)
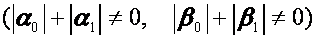 ,
,
где 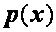 ,
, 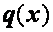 , и
, и 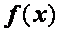 непрерывны на [ a, b ].
непрерывны на [ a, b ].
Разобьем отрезок [ a, b ] на n равных частей длины, или шага
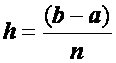 .
.
Точки разбиения
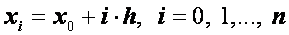 ,
, 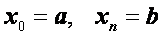
называются узлами, а их совокупность – сеткой на отрезке [ a, b ]. Значения в узлах искомой функции 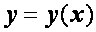 и ее производных
и ее производных 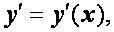
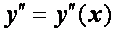 обозначим соответственно через
обозначим соответственно через
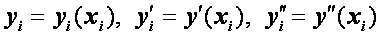 .
.
Введем обозначения
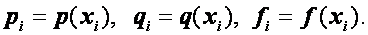
Заменим производные так называемыми односторонними конечно-разностными отношениями:
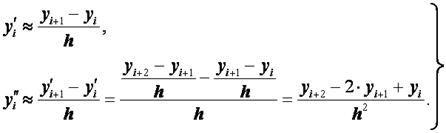 (2.26)
(2.26)
Формулы (2.26) приближенно выражают значения производных во внутренних точках интервала [ a, b ].
Для граничных точек положим
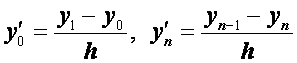 . (2.27)
. (2.27)
Используя формулы (2.26), дифференциальное уравнение (2.24) при 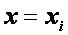 , (i = 1, 2,..., n –1) приближенно можно заменить линейной системой уравнений
, (i = 1, 2,..., n –1) приближенно можно заменить линейной системой уравнений
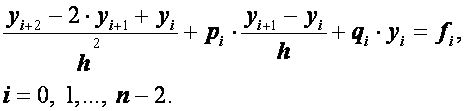 (2.28)
(2.28)
Кроме того, в силу формул (2.27) краевые условия (2.25) дополнительно дают еще два уравнения:
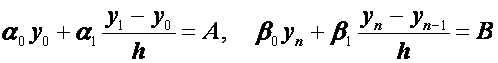 . (2.29)
. (2.29)
Таким образом, получена линейная система n + 1 уравнений с n + 1 неизвестными 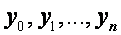 , представляющими собой значения искомой функции
, представляющими собой значения искомой функции 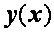 в узлах сетки. Система уравнений (2.28), (2.29), заменяющая приближенно дифференциальную краевую задачу (2.24), (2.25) обычно называется разностной схемой. Решить эту систему можно каким-либо общим численным методом. Однако схема (2.28), (2.29) имеет специфический вид и ее можно эффективно решить специальным методом, называемым методом прогонки. Специфичность системы заключается в том, что уравнения ее содержат три соседних неизвестных и матрица этой системы является трехдиагональной.
в узлах сетки. Система уравнений (2.28), (2.29), заменяющая приближенно дифференциальную краевую задачу (2.24), (2.25) обычно называется разностной схемой. Решить эту систему можно каким-либо общим численным методом. Однако схема (2.28), (2.29) имеет специфический вид и ее можно эффективно решить специальным методом, называемым методом прогонки. Специфичность системы заключается в том, что уравнения ее содержат три соседних неизвестных и матрица этой системы является трехдиагональной.
Преобразуем уравнения (2.28):
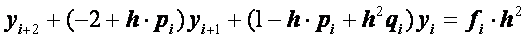 . (2.30)
. (2.30)
Введя обозначения
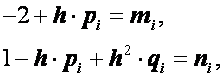
получим
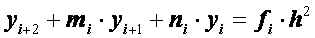 , (i =0, 1,..., n -2).(2.31)
, (i =0, 1,..., n -2).(2.31)
Краевые условия по-прежнему запишем в виде
 . (2.32)
. (2.32)
Метод прогонки состоит в следующем.
Разрешим уравнение (2.31) относительно 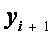 :
:
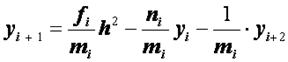 . (2.33)
. (2.33)
Предположим, что с помощью полной системы (2.31) из уравнения исключен член, содержащий 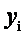 . Тогда уравнение (2.33) может быть записано в виде
. Тогда уравнение (2.33) может быть записано в виде
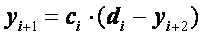 , (2.34)
, (2.34)
где 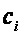 и
и 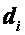 должны быть определены. Найдем формулы для этих коэффициентов. При i = 0 из формулы (2.33) и краевых условий (2.32) следует, что
должны быть определены. Найдем формулы для этих коэффициентов. При i = 0 из формулы (2.33) и краевых условий (2.32) следует, что
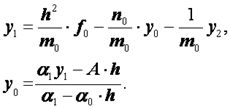
Исключая из этих двух уравнений 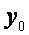 , найдем
, найдем
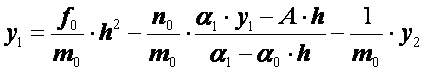 .
.
Выразим теперь отсюда 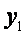 :
:
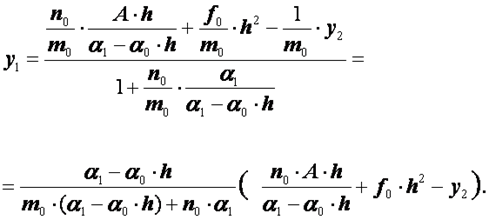 (2.35)
(2.35)
Но, согласно формуле (2.34),
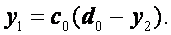 (2.36)
(2.36)
Сравнивая теперь (2.35) и (2.36), найдем, что
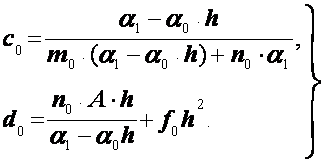 (2.37)
(2.37)
Пусть теперь i > 0, то есть i = 1, 2,..., n– 2. Выражая 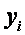 по формуле (2.34), получим:
по формуле (2.34), получим:
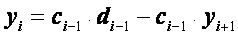 .
.
Подставляя это в формулу (2.33), будем иметь
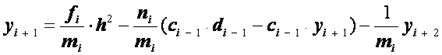 .
.
Разрешая полученное уравнение относительно 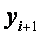 , находим
, находим
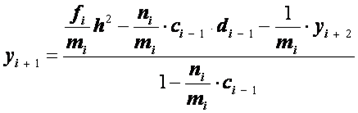 , или
, или
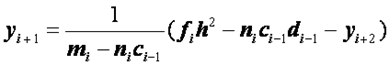 . (2.38)
. (2.38)
Отсюда, сравнивая формулы (2.34) и (2.38), получаем для коэффициентов 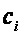 и
и 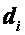 рекуррентные формулы:
рекуррентные формулы:
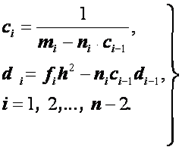 (2.39)
(2.39)
Так как 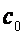 и
и 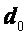 уже определены по формулам (2.37), то, используя формулы (2.39), можно последовательно определить коэффициенты
уже определены по формулам (2.37), то, используя формулы (2.39), можно последовательно определить коэффициенты 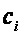 и
и 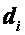 до
до 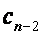 и
и 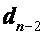 включительно. Эти вычисления называются прямым ходом метода прогонки.
включительно. Эти вычисления называются прямым ходом метода прогонки.
Из формулы (2.33) при i=n– 2 и второго краевого условия (2.32) получаем

Разрешая эту систему относительно 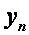 , будем иметь
, будем иметь
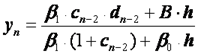 . (2.40)
. (2.40)
Теперь, используя (2.34) и первое краевое условие (2.32), мы можем последовательно найти 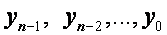 . Это − обратный ход метода прогонки.
. Это − обратный ход метода прогонки.
Итак, получаем следующую цепочку:
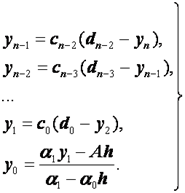 (2.41)
(2.41)
Для простейших краевых условий 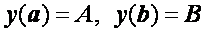
формулы для 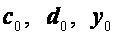 и
и 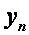 упрощаются. Полагая в этом случае
упрощаются. Полагая в этом случае 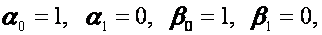 из формул (2.37), (2.40), (2.41) будем иметь
из формул (2.37), (2.40), (2.41) будем иметь
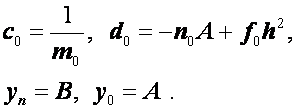
Рассмотренный нами подход сводит линейную краевую задачу к системе линейных алгебраических уравнений. При этом возникает три вопроса.
1) Существует ли решение алгебраической системы типа (2.31)?
2) Как фактически находить это решение?
3) Сходится ли разностное решение к точному при стремлении шага сетки к 0?
Можно доказать, что если краевая задача имеет вид
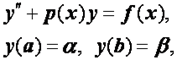
причем р (x) > 0, то решение системы (2.31), (2.32) существует и единственно. Фактическое отыскание решения можно провести, например, методом прогонки. На третий вопрос дает ответ следующая
 2015-01-07
2015-01-07 1158
1158