Теорема

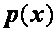Если и 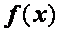дважды непрерывно дифференцируемы, то разностное решение, соответствующее схеме с заменой

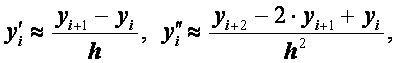
равномерно сходится к точному с погрешностью 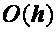при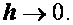

Таким образом, схема (2.28), (2.29) дает приближенное решение краевой задачи, но точность ее весьма мала. Это связано с тем, что аппроксимация производной

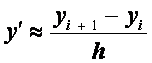
имеет низкий порядок точности − погрешность этой аппроксимации

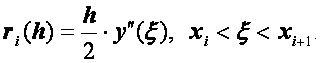
Более точную разностную схему можно получить, если при переходе от линейной краевой задачи к конечно-разностным уравнениям воспользоваться центральными формулами для производных:

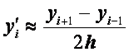, (2.42)

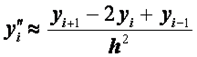, (2.43)

i = 1, 2,..., n.

Погрешность формулы (2.42) выражается так:

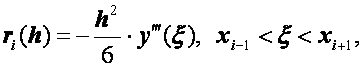
то есть формула (2.42) имеет второй порядок точности относительно шага сетки h. Подставляя выражения (2.42), (2.43) в задачу (2.24), (2.25) и выполняя некоторые преобразования, получим следующую систему:

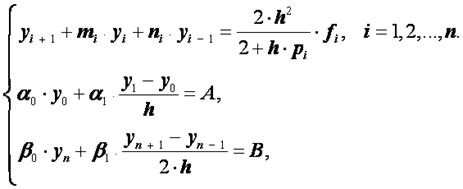(2.44)

Где .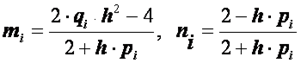

Система (2.44) снова трехдиагональная и ее решение также можно получить методом прогонки. Его алгоритм здесь будет выглядеть так. Сначала находят коэффициенты

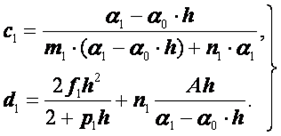(2.45)

Затем определяют коэффициенты 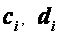по следующим рекуррентным формулам:

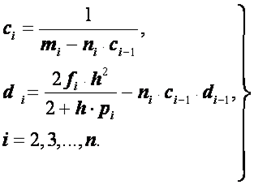(2.46)

Обратный ход начинается с нахождения :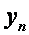

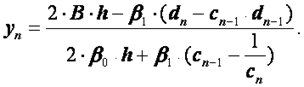(2.47)

После этого находим 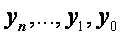по формулам:

, (2.48)

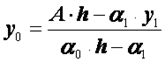. (2.49)

Относительно схемы (2.44) можно также доказать, что она имеет единственное решение пр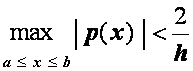и

и ,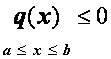

и это решение может быть найдено описанным методом прогонки. Кроме того, для схемы (2.44) имеет место