Примитивно-рекурсивными могут быть не только арифметические функции, но и «арифметизованные» логические функции, отношения, предикаты, операторы.
«Арифметизованная» логическая функция – это такая числовая арифметическая функция, которая на множестве { 0,1 } ведет себя также, как логическая.
Операции 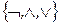 на множестве { 0,1 } примитивно-рекурсивны.
на множестве { 0,1 } примитивно-рекурсивны. 
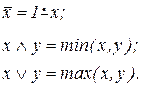
Функции 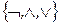 на множестве {0,1} образуют базис, следовательно, все остальные арифметизованные логические функции могут быть представлены в виде суперпозиции этих трёх функций, а, следовательно, по определению примитивной рекурсивности они примитивно-рекурсивны.
на множестве {0,1} образуют базис, следовательно, все остальные арифметизованные логические функции могут быть представлены в виде суперпозиции этих трёх функций, а, следовательно, по определению примитивной рекурсивности они примитивно-рекурсивны.
Отношение 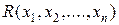 называется примитивно-рекурсивным, если примитивно-рекурсивна его характеристическая функция
называется примитивно-рекурсивным, если примитивно-рекурсивна его характеристическая функция 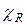 :
:
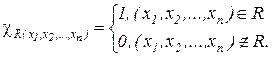
Пример 11. Отношение 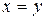 – примитивно-рекурсивно.
– примитивно-рекурсивно.
Действительно, 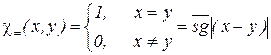 .
.
Отношение 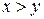 примитивно-рекурсивно.
примитивно-рекурсивно.
Действительно, 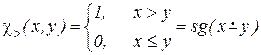 .
.
Отношение 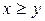 примитивно-рекурсивно.
примитивно-рекурсивно.
Действительно, 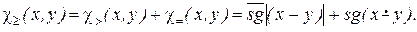
Предикат – функция, определяющая обладают ли ее аргументы свойством или нет и возвращает значение: 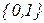 , {“false”,“true”}, {“ложь”, ”истина”}.
, {“false”,“true”}, {“ложь”, ”истина”}.
Предикат 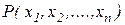 называется примитивно-рекурсивным, если примитивно-рекурсивна его характеристическая функция:
называется примитивно-рекурсивным, если примитивно-рекурсивна его характеристическая функция:
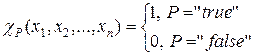 .
.
Оператор называется примитивно-рекурсивным, если он сохраняет примитивную рекурсивность функций, т.е. если результат его применения к примитивно-рекурсивным функциям дает снова примитивно-рекурсивную функцию.
Пример 12. Примитивная рекурсивность оператора условного перехода
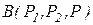 .
.
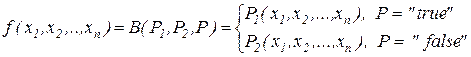
где 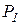 и
и 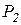 – примитивно-рекурсивные функции; P – примитивно-рекурсивный предикат. Примитивная рекурсивность функции
– примитивно-рекурсивные функции; P – примитивно-рекурсивный предикат. Примитивная рекурсивность функции 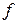 (оператора B) следует из равенства:
(оператора B) следует из равенства:
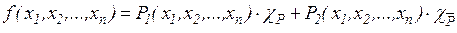
 2015-01-07
2015-01-07 4043
4043
