В качестве простейших функций в теории рекурсивных функций приняты следующие:
1. 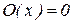 – константа «ноль».
– константа «ноль».
2. 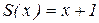 – «последователь».
– «последователь».
3. 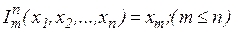 – функция тождества или выбора аргумента, проекция.
– функция тождества или выбора аргумента, проекция.
Оператор суперпозиции (подстановки) 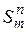 – подстановка в функцию от
– подстановка в функцию от 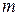 переменных
переменных 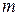 функций от
функций от 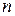 переменных, что дает новую функцию от
переменных, что дает новую функцию от 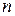 переменных.
переменных.
Суперпозицией функций 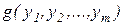 и
и 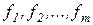 называют функцию:
называют функцию:
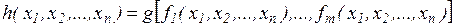 ;
;
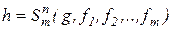 .
.
Оператор примитивной рекурсии 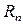 , определяющий значение функции
, определяющий значение функции 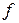 , записывается в виде следующей схемы:
, записывается в виде следующей схемы:
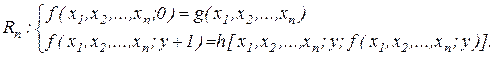
Частные случаи:
при n= 1 имеем 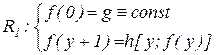 ,
,
при n= 2 имеем 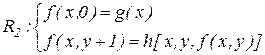 .
.
Примитивно-рекурсивная функция – арифметическая функция, которая может быть получена из простейших с помощью конечного числа применений операторов суперпозиции и примитивной рекурсии.
Примитивно-рекурсивные функции являются всюду определенными.
Пример 1. Вычислить функцию 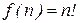 с помощью оператора примитивной рекурсии:
с помощью оператора примитивной рекурсии:
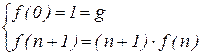
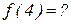
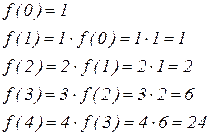
Пример 2. Вычислить функцию 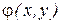 с помощью оператора примитивной рекурсии:
с помощью оператора примитивной рекурсии:
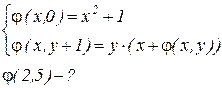
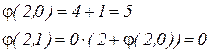
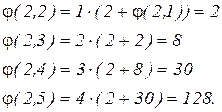
Для того чтобы показать, что какая-либо функция является примитивно-рекурсивной, достаточно построить ее согласно определению. Однако такое построение получается слишком сложным и громоздким. Поэтому в большинстве случаев заданную функцию пытаются выразить с помощью операторов суперпозиции и примитивной рекурсии через другие функции, примитивная рекурсивность которых доказана ранее. Приведем примеры доказательства примитивной рекурсивности некоторых простых арифметических функций.
Пример 3. Константа 1 может быть получена суперпозицией двух простейших функций: константы «ноль» и функции «последователь»:
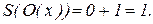
Пример 4. Константа a получается суперпозиции функций 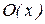 и
и 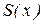 :
:
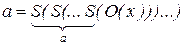
Пример 5. Операция сложения 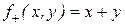 может быть определена с помощью оператора примитивной рекурсии:
может быть определена с помощью оператора примитивной рекурсии:
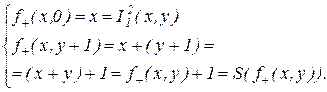
Пример 6. Примитивная рекурсивность операции умножения 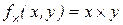 доказывается через операцию сложение:
доказывается через операцию сложение:
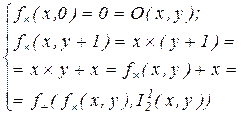
Пример 7. Примитивная рекурсивность операции возведения в степень 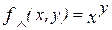 доказывается следующим образом:
доказывается следующим образом:
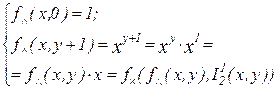
Пример 8. Операция вычитания не является примитивно-рекурсивной, т.к. она не всюду определена: результат операции a-b при 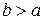 не определен в области натуральных чисел. Однако примитивно-рекурсивной является так называемое арифметическое (усеченное) вычитание или разность.
не определен в области натуральных чисел. Однако примитивно-рекурсивной является так называемое арифметическое (усеченное) вычитание или разность.
Арифметическое вычитание:
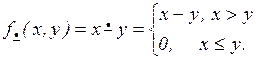
Для доказательства примитивной рекурсивности 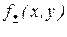 вначале рассмотрим операцию
вначале рассмотрим операцию 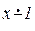 :
: 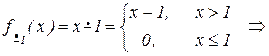 ;
;
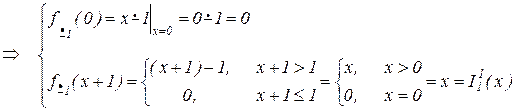
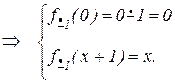
т.е. операция 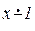 – примитивно-рекурсивна.
– примитивно-рекурсивна.
Дополнительное свойство: 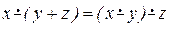 .
.
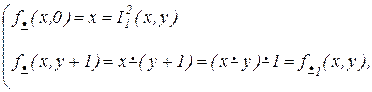
арифметическое вычитание – примитивно-рекурсивно.
Пример 9. Функция 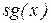 – аналог функции
– аналог функции 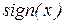 для натуральных чисел.
для натуральных чисел.
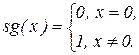
Функция 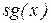 примитивно-рекурсивна:
примитивно-рекурсивна:
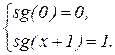
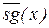 – антисигнум, функция обратная
– антисигнум, функция обратная 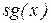 .
.

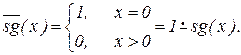 .
.
Пример 10. Примитивная рекурсивность функций 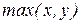 ,
, 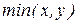 и модуль двух чисел доказывается с помощью арифметического вычитания:
и модуль двух чисел доказывается с помощью арифметического вычитания:
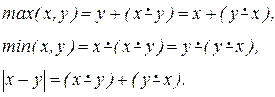
 2015-01-07
2015-01-07 15674
15674








