Методы Монте-Карло

1) 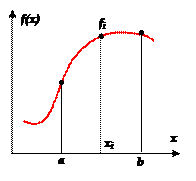одномерная случайная величина – статистический вариант метода прямоугольников.

В качестве текущего узла x_i берется случайное число, равномерно распределенное на интервале интегрирования [ a, b ]. Проведя N вычислений, значение интеграла определим по следующей формуле: 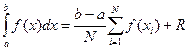. Для R можно утверждать хотя бы ~ .

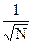2) двумерная случайная величина ­– оценка площадей.

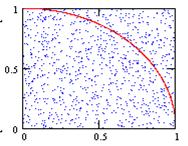
Рассматриваются две равномерно распределенных случайных величины x _i и y _i, которые можно рассматривать как координаты точки в двумерном пространстве. За приближенное значение интеграла принимается количества точек S, попавших под кривую y = f (x), к общему числу испытаний N, т.е. .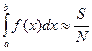

И первый, и второй случай легко обобщаются на кратные интегралы.