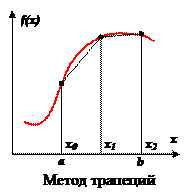
Различают метод левых, правых и средних прямоугольников. Суть метода ясна из рисунка. На каждом шаге интегрирования функция аппроксимируется полиномом нулевой степени – отрезком, параллельным оси абсцисс.
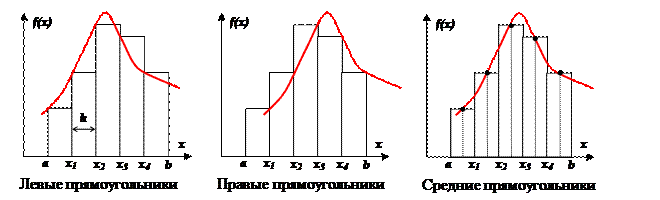
Выведем формулу метода прямоугольников из анализа разложения функции f(x) в ряд Тейлора вблизи некоторой точки x = x i.
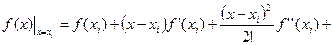 …
…
Рассмотрим диапазон интегрирования от x i до x i + h, где h – шаг интегрирования.
Вычислим 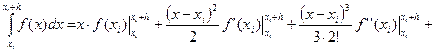 …=
…=
= 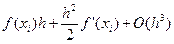 =
= 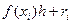 . Получили формулу правых (или левых) прямоугольников и априорную оценку погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма – степень при величине шага в формуле априорной оценки погрешности.
. Получили формулу правых (или левых) прямоугольников и априорную оценку погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма – степень при величине шага в формуле априорной оценки погрешности.
В случае равного шага h на всем диапазоне интегрирования общая формула имеет вид
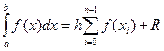 .
.
Здесь n – число разбиений интервала интегрирования, 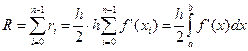 . Для справедливости существования этой оценки необходимо существование непрерывной f’ (x).
. Для справедливости существования этой оценки необходимо существование непрерывной f’ (x).
Метод средних прямоугольников. Здесь на каждом интервале значение функции считается в точке 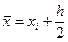 , то есть
, то есть 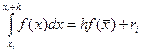 . Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше:
. Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше:
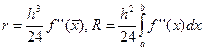 .
.
 2015-01-07
2015-01-07 695
695








