Метод оврагов

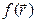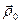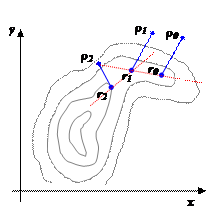
Ставится задача найти минимум для овражной функции. Для этого выбираются две близкие точки и 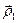, и осуществляется спуск из этих точек (любым методом), причем высокой точности сходимости не требуется. Конечные точки спуска 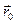и 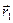будут лежать вблизи дна оврага. Затем осуществляется движение вдоль прямой, соединяюще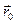й и 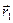в сторону уменьшения 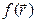(как бы вблизи дна оврага). Движение может быть осуществлено только на один шаг ~ h, направление выбирается из сравнения значения функции в точках 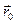и 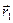. Таким образом, находится новая точка 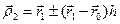. Так как возможно, что точка 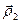уже лежит на склоне оврага, а не на дне, то из нее снова осуществляется спуск в новую точку 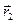. Затем намечается новый путь по дну оврага вдоль прямой, соединяюще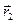й и 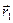. Если 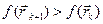– процесс прекращается, а в качестве минимума в данном овраге используется значение .

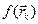Метод оврагов рассчитан на то, чтобы пройти вдоль оврага и выйти в котловину около минимума. В этой котловине значения минимума лучше уточнять другими методами.