Общие сведения. Цель работы - приобретение практических навыков в планировании и проведении экспериментов при поиске параметров линейной модели сложной системы

Работа 1. ПЛАНИРОВАНИЕ ДРОБНОГО ФАКТОРНОГО ЭКСПЕРИМЕНТА

Цель работы - приобретение практических навыков в планировании и проведении экспериментов при поиске параметров линейной модели сложной системы управления.

Порядок выполнения работы

Работу следует выполнять в таком порядке:

1. Подготовить исходные данные для проведения эксперимента (вари­анты исходных данных приведены в табл. 1.3):

— составить модель локального участка целевой функции;

— выбрать положение локального участка и интервалы варьирова­ния;

— выбрать дробность реплики и составить план проведения экспери­мента.

2. Провести эксперимент:

— определить на модели исследуемого объекта («черного ящика») значения целевой функции;

— вычислить коэффициенты регрессии;

— проверить коэффициенты регрессии на значимость;

— проверить адекватность модели.

3. Оформить бригадный отчет о работе.

4. Ответить на контрольные вопросы.

Общие сведения

Статистические методы планирования активного эксперимента явля­ются одним из эмпирических способов получения математического описа­ния сложных объектов исследования, т.е. уравнения связи отклика объекта у и независимых управляемых входных переменных (факторов) х=(x₁,x₂,…,x_k).

При этом математическое описание представляется в виде некоторого полинома — отрезка ряда Тейлора, в который разлагается неизвестная зависимость в окрестности основной точки x, например:

M{y}=j(x₁,x₂,…,x_n)=b₀+åb_jx_j+åb_jlx_jx_l+åb_jjx_j², j,l=1..k, l<j (1.1)

где b_j,b_jl ,b_jj – теоретические коэффициенты:

; ;

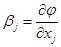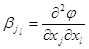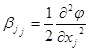
Вследствие наличия неуправляемых и даже неконтролируемых факто­ров изменение величины у носит случайный характер, поэтому функцио­нальная зависимость j(x) не дает точной связи между управляемыми факторами x⁽ⁱ⁾и откликом объекта y_i, в каждом i-м опыте, а лишь между управляемыми факторами и математическим ожиданием случайной вели­чины y:

M{y_i}=j(x⁽ⁱ⁾) (1.2)

где j(x) – уравнение регрессии у по х; x⁽ⁱ⁾=(x₁⁽ⁱ⁾, x₂⁽ⁱ⁾,…, x_n⁽ⁱ⁾) – i-я точка пространства независимых управляемых факторов (факторного пространства).

В таком случае по результатам эксперимента можно отыскать оценку уравнения регрессии у=j(x) в форме некоторого полинома

у^М=b₀+åb_jx_j+åb_jlx_jx_l+åb_jjx_j², j,l=1..k, l<j (1.3)

где коэффициенты b₀, b₁,…, b_j,…, b_jjявляются лишь оценками теоре­тических коэффициентов регрессии b₀, b₁, b_j, b_jj соответственно, а у^М — оценкой М{y}, вычисленной по уравнению регрессии (1.3). Пусть x⁽ⁱ⁾(i=1,N)— точки факторного пространства, в которых проводится эксперимент. Тогда задача отыскания оценок коэффициентов уравнения регрессии (1.3) по результатам опытов в N точках факторного пространст­ва является типичной задачей множественного регрессионного анализа в том случае, если выполняются следующие предпосылки:

1. Результаты наблюдений отклика y₁, y₂,…, y_N в N точках фактор­ного пространства представляют собой независимые нормально распреде­ленные случайные величины, т.е. на них воздействуют нормально распре­деленные случайные помехи x, с нулевым математическим ожиданием M[x].

2. Дисперсии s²{y₁} (i=1,N) равны. Это значит, что дисперсия s²{y₁} не зависит от значения входных переменных x и получаемые при проведении многократных повторных наблюдений над величиной yв любых точках x⁽ⁱ⁾факторного пространства выборочные оценки диспер­сии s_i (у) однородны (воспроизводимость с равной точностью).

3. Независимые управляемые факторы x₁, x₂,…, x_kизмеряются с пренебрежимо малыми ошибками по сравнению с ошибкой x, в определе­нии у (имеется в виду влияние их ошибок на величину у по сравнению с влиянием неуправляемых и неконтролируемых факторов).

Для локального участка в пределах заданной точности поверхность отклика может быть аппроксимирована полиномом первой степени

y^M=b₀+åb_jx_j j=0..k (1.4)

Положение локального участка задается координатами базовой (центральной) точки (x₁₀, x₂₀,…, x_k0), называемой центром экспери­мента, и величиной интервалов варьирования Dx₁, Dx₂,…, Dx_k.

Выбор координат базовой точки должен отвечать следующим услови­ям:

— центр эксперимента принимается в точке обычного номинального режима

функционирования исследуемой системы (объекта);

— базовая точка может находиться в центре области ограничения факторов х_i, если они имеются в наличии, а другой информации о целевой функции нет;

— если имеется какая-то информация относительно положения экс­тремума целевой функции, то целесообразно центр эксперимента выбрать вблизи предполагаемого оптимума.

Интервалы варьирования выбираются исходя из следующих сообра­жений. Большие интервалы варьирования не позволяют определить осо­бенности поверхности отклика. Слишком малые интервалы обусловлива­ют рост погрешностей в оценке составляющих градиента за счет возраста­ния ошибки наблюдений. Кроме того, необходимо, чтобы входные и вы­ходные переменные не выходили за допустимую область:

x_{j min}£x_j£x_{j max}, j=1,k (1.5)

где x_{j min}, x_{j max} — нижняя и верхняя границы изменения j-го фактора.

В общем случае выбор локального участка (центра плана и интерва­лов варьирования) зависит от вида поверхности отклика. В лабораторной работе начальные координаты центра плана принимаются равными сере­дине области определения факторов, а начальные значения интервалов варьирования обычно принимаются равными 1...5% от величины указан­ной области.

При построении плана эксперимента в локальной области факторно­го пространства используется кодировка уровней факторов с помощью формулы

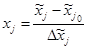
где х_j— кодированное значение уровня фактора; х_j^~ — реальное значение уровня фактора в натуральных единицах; х_j0^~ — значение фактора в центре плана в натуральных единицах; D x _j^~— интервал варьирования в натуральных единицах.

Если число факторов известно и планирование проводится на двух уров­нях, то число опытов, необходимое для реализации всех возможных ком­бинаций уровней факторов, будет

N=2^k

Условия эксперимента можно записать в виде таблицы, где строки соответствуют различным опытам, а столбцы — значениям факторов. На­пример, для двух факторов условия эксперимента приведены в табл. 1.1.

Таблица 1.1

Номер	Фактор		Отклик
	х1	х2	у
	-1	-1	у1
	+1	-1	у2
	-1	+1	у3
	+1	+1	у4

Сформированный подобным образом план эксперимента называется

двухуровневым полным факторным экспериментом (ПФЭ) типа 2^k. Для его построения можно воспользоваться следующим приемом: в первом столбце знаки меняются поочередно, во втором — чередуются через два, в третьем — через четыре, в четвертом — через восемь и т.д.

План, соответствующий построенной таким образом матрице плани­рования (МП), обладает следующими свойствами:

1) симметричность относительно центра эксперимента — алгебраи­ческая сумма элементов вектор-столбца каждого фактора равна нулю:

åx⁽ⁱ⁾_j=0, i=1,N, j=1,k

2) условие нормировки — сумма квадратов элементов каждого столб­ца равна числу опытов:

å (x⁽ⁱ⁾_j)²=N, i=1,N, j=1,k

3) ортогональность матрицы — скалярное произведение любых двух векторов-столбцов матрицы равна нулю:

åx⁽ⁱ⁾_j* x⁽ⁱ⁾_u =0, j¹u, i=1,N, j,u=1,k

Полный факторный эксперимент дает возможность вычислить неза­висимо коэффициенты, соответствующие не только линейной части моде­ли (1.1), но и эффектам взаимодействия. Во многих практических задачах влияние взаимодействий (произведений факторов) второго и более высо­ких порядков отсутствует или пренебрежимо мало. Кроме того, на первых этапах исследования часто достаточно получить в первом приближении лишь линейную аппроксимацию изучаемого уравнения связи при мини­мальном количестве опытов. Поэтому неэффективно использовать ПФЭ для оценивания коэффициентов лишь при линейных членах и некоторых парных произведениях из-за избыточного числа точек плана (2^k), в осо­бенности при большом числе факторов k (для определения (k+1) коэффи­циентов линейной модели достаточно (k + 1) точек плана эксперимента).

Дробным факторным экспериментом (ДФЭ) называется эксперимент, реализующий часть (дробную реплику) полного факторного эксперимен­та. Он позволяет получить, например, линейное приближение искомой функциональной зависимости М {у} = j(х) в некоторой небольшой ок­рестности точки базового режима при меньшем числе опытов.

Так, для решения трехфакторной (k = 3) задачи регрессии в линейном приближении можно ограничиться четырьмя вариантами варьирования, если для плана ПФЭ типа 2² переменных х ₁, х ₂ произведение х ₁, х ₂ приравнять третьему независимому фактору х ₃. Использование матрицы планирования, представленной в табл. 1.2, позволяет найти свободный член b₀ и три оценки коэффициентов регрессии при линейных членах

b₁, b₂, b₃ (из четырех опытов нельзя получить более четырех оценок коэффициентов регрессии).

Таблица 1.2

n	X0	X1	X2	X3	X1 X2	X1 X3	X2 X3	X1X2X3
	+1	-1	-1	+1	+1	-1	-1	+1
	+1	+1	-1	-1	-1	-1	+1	+1
	+1	-1	+1	-1	-1	+1	-1	+1
	+1	+1	+1	+1	+1	+1	+1	+1

Применение ДФЭ всегда связано со смешиванием, т.е. с совместным оцениванием нескольких теоретических коэффициентов математической модели. В рассматриваемом случае каждый из найденных коэффициентов b₁ включает в себя оценки двух теоретических коэффициентов регрессии:

b₀®b₀+b₁₂₃; b₁®b₁+b₂₃; b₂®b₂+b₁₃; b₃®b₃+b₁₂;

Действительно, указанные теоретические коэффициенты в таком пла­нировании не могут быть найдены раздельно, поскольку столбцы МП для линейных членов и парных произведений совпадают (полностью коррелированы). Рассмотренный план ДФЭ представляет половину плана ПФЭ типа 2 ³ и называется полурепликой от ПФЭ типа 2 ³ или планом типа N = 2^3-1 (табл. 1.2).

При большом числе k факторов для получения линейного приближе­ния можно построить дробные реплики более высокой степени дробности. Так, при k= 5 можно составить дробную реплику (четвертьреплику) на основе ПФЭ типа 2 ³, приравняв два из пяти факторов к взаимодействиям трех других факторов: парному и тройному. Будем обозначать тип дроб­ной реплики записью 2 ^k-p, если р факторов приравнены к произведени­ям остальных k - р факторов. Дробность реплики при этом равна

1/2^p.

При планировании ДФЭ недопустимо произвольное разбиение ПФЭ на части. Для правильного планирования ДФЭ необходимо использовать все имеющиеся сведения теоретического и интуитивного характера об объекте и выделить те факторы и произведения факторов, влияние кото­рых на отклик существенно. При этом смешивание нужно производить так, чтобы линейные коэффициенты b₀, b₁, …, b_k были смешаны с коэффициентами при взаимодействиях самого высокого порядка (так как обычно они в модели отсутствуют) или при тех взаимодействиях, о кото­рых априори известно, что они не оказывают влияния на отклик.

Для построения плана ДФЭ типа 2 ^k-p выбирается k - р факторов и для них строится ПФП. Значения оставшихся p факторов определяются приравниванием их различным взаимодействиям (парным, тройным и т.д.) предшествующих факторов. Эти выражения называются генерирую­щими соотношениями. Так, в рассмотренном выше примере при построении полуреплики типа 2 ^3-1 переменная x была задана генерирующим соотношением х₃ = х₁ х₂.

Умножив обе части генерирующего соотношения на переменную, для задания которой оно использовалось, получим выражение, называемое определяющим контрастом (1 = х ₁ х ₂ х ₃, так как всегда х ₁ х ₁ = 1). Совокупность всех определяющих контрастов, а также их произведений составляет обобщающий определяющий контраст (ООК).

Значение ООК позволяет для всех факторов определить, с какими эффектами взаимодействия смешаны их линейные эффекты. Перемножив поочередно каждый из независимых факторов на ООК, получим x₁=x₂x₃, x₂=x₁x₃, x₃=x₁x₂.Собственно сам ООК зада­ет систему смешивания для центра плана x₀=x₁x₂x_3.

Отсюда легко находятся смешиваемые теоретические коэффициенты регрессии и их оценки:

b₀®b₀+b₁₂₃; b₁®b₁+b₂₃; b₂®b₂+b₁₃; b₃®b₃+b₁₂;

Если априори можно принять, что коэффициенты при всех парных и тройном взаимодействиях равны нулю, то реализация этой полуреплики позволит получить раздельные оценки всех четырех линейных коэффици­ентов регрессии.

Для четвертьреплики в пятифакторном планировании типа 2^5-2 должны быть заданы два генерирующих соотношения, например:

x₄=x₁x₂x₃, x₅=x₁x₂,

причем полагаем b₁₂₃= 0, т.е. x₁,x₂,x₃ все вместе не взаимодейст­вуют и b₁₂= 0, т.е. x₁,x₂также не взаимодействуют. Определяющие контрасты для этой реплики согласно приведенным выше правилам имеют вид

1=x₁x₂x₃x₄, 1=x₁x₂x₅

Обобщающий определяющий контраст, построенный на основе всех полученных определяющих контрастов и их произведений, полностью характеризует разрешающую способность реплик высокой степени дроб­ности. Так, в данном случае ООК имеет вид

1= x₁x₂x₃x₄= x₁x₂x₅=x₃x₄x₅.

Совместные оценки здесь определяются вспомогательными соотно­шениями

x₀=x₁x₂x₃x₄=x₁x₂x₅=x₃x₄x₅;

x₁=x₂x₃x₄=x₂x₅=x₁x₃x₄x₅;

x₂=x₁x₃x₄=x₁x₅=x₂x₃x₄x₅;

x₁x₃=x₂x₄=x₂x₃x₄=x₁x₄x₅;

x₃=x₁x₂x₄=x₁x₂x₃x₅=x₄x₅;

x₄=x₁x₂x₃=x₁x₂x₄x₅=x₃x₅;

x₅=x₁x₂x₃x₄x₅=x₁x₂=x₃x₄;

Эти вспомогательные соотношения позволяют установить, какие столбцы МП окажутся линейно зависимыми и, следовательно, совместной оценкой каких теоретических коэффициентов является тот или иной выбо­рочный коэффициент регрессии:

b₀®b₀+b₁₂₃₄+b₁₂₅+b₃₄₅;

b₁®b₁+b₂₃₄+b₂₅+b₁₃₄₅;

b₂®b₂+b₁₃₄+b₁₅+b₂₃₄₅;

b₃®b₃+b₁₂₄+b₁₂₃₅+b₄₅;

b₄®b₄+b₁₂₃+b₁₂₄₅+b₃₅;

b₅®b₅+b₁₂₃₄₅+b₁₂+b₃₄;

b₁₃®b₁₃+b₂₄+b₂₃₅+b₁₄₅;

b₁₄®b₁₄+b₂₃+b₂₄₅+b₁₃₅;

Разрешающая способность этой четвертьреплики невысокая и равна трем, так как все теоретические линейные коэффициенты регрессии сме­шаны с коэффициентами при парных взаимодействиях. Следует иметь в виду, что план ДФЭ всегда можно дополнить до плана ПФЭ недостающи­ми дробными репликами. В данном примере для остальных трех четвертьреплик генерирующие соотношения запишутся в виде

x₄=x₁x₂x₃;

x₅=-x₁x₂;

x₄=-x₁x₂x₃;

x₅=x₁x₂;

x₄=-x₁x₂x₃;

x₅=-x₁x₂;

а обобщающие определяющие соотношения — в виде

1=x₁x₂x₃x₄=-x₁x₂x₅=-x₃x₄x₅;

1=-x₁x₂x₃x₄=-x₁x₂x₅=-x₃x₄x₅;

1=-x₁x₂x₃x₄=-x₁x₂x₅=x₃x₄x₅;

Осуществление этих дополняющих четвертьреплик означает реализа­цию ПФЭ в целом и, следовательно, раздельное оценивание всех теорети­ческих коэффициентов регрессии.

С учетом свойств матрицы планирования формулы для вычисления оценок коэффициентов регрессии b_j и b_j1 принимают вид

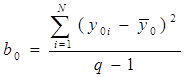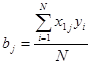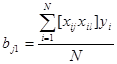; ; ; j,l=1,..,k, j¹l (1.6)

Поскольку они определяются по результатам эксперимента (случай­ные величины), то и значения их также случайны, т.е. определяются с погрешностями. Может случиться, что абсолютная величина некоторых коэффициентов приблизительно равна погрешностям их определения или даже меньше. Такие коэффициенты считаются незначимыми. Физически незначимость коэффициента по какому-либо фактору х_j означает, что приращение целевой функции, вызванное изменением фактора х_j, соиз­меримо с погрешностями измерения целевой функции.

Для ортогональных планов ПФЭ и ДФЭ дисперсии коэффициентов регрессии равны между собой и определяются следующим образом:

s_bj²=s_bjl²=Dвос/N,

где Dвос - s ²{у} — дисперсия воспроизводимости, характеризующая

ошибку наблюдений. Для ее определения в одной из точек плана (обычно в центре) производится q независимых наблюдений выходной переменной у. Оценка Dвос будет

;

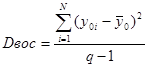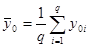
где у _0j — значение выходной переменной в i-м наблюдении.

Проверка значимости коэффициентов b j состоит в проверке статис­тической гипотезы H₀: bj = 0. С этой целью используется статистика

U j=b_j/ s_bj, подчиненная t-распределению Стьюдента c n_вос =q -1 числом степеней свободы. Если вычисленное значение ½ U j ½< t_a, то гипотеза принимается и коэффициент bj незначим. Значение t_a берется из таблицы t -распределения (приложение 2) при заданном уровне значи­мости a.

Аналогично может быть проверена значимость коэффициентов рег­рессии b_jl.

Статистическая незначимость оценки коэффициента регрессии может быть обусловлена следующими причинами:

— данный j-й фактор не имеет функциональной связи с откликом, т.е. b_j = 0;

— уровень х_j0 базового режима x₀ находится в точке частного экстремума функции отклика по фактору xj и тогда

b_j=¶y/¶x_j=0;

— интервал варьирования D x_jвыбран малым;

— вследствие влияния неуправляемых и неконтролируемых факторов велика ошибка воспроизводимости эксперимента.

Если значимы все коэффициенты регрессии, полученная модель может быть использована для исследования системы.

Если часть коэффициентов регрессии значима, а часть незначима, то можно провести дополнительную серию опытов с тем же центром плана (или с его переносом) и новыми интервалами варьирования по незначи­мым факторам.

Возможны другие способы получения значимых коэффициентов — увеличение числа параллельных опытов и достройка плана путем перехода к реплике меньшей дробности.

Если все коэффициенты незначимы, следует увеличить интервалы варьирования D х_j (j=1,k) по всем факторам.

Следует отметить, что найденные по формулам (1.6) параметры моде­ли могут быть использованы только при подстановке в модель (1.4) нор­мированных значений переменных (1.5). Для получения линейной регрес­сионной модели, использующей значения входных переменных в нату­ральных единицах, необходимо произвести пересчет коэффициентов мо­дели по формулам

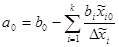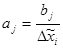; ; j=1,..,k

где b — коэффициенты модели в нормированной системе координат; а — коэффициенты модели в абсолютной системе координат.

Для модели первого порядка с парными взаимодействиями формулы пересчета коэффициентов имеют вид

;

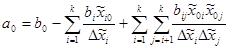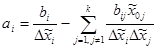, i=1..k;

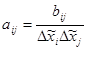, i,j=1..k, i>j

Для проверки гипотезы об адекватности математического описания опытным данным достаточно оценить отклонение предсказаний по полу­ченному уравнению регрессии величины отклика у^M_i от результатов на­блюдений y_i в одних и тех же i -x точках факторного пространства. Рас­сеяние результатов наблюдений вблизи уравнения регрессии, оцениваю­щего истинную функцию отклика, можно охарактеризовать с помощью дисперсии адекватности

,

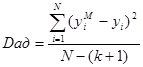где (k + 1) — число членов аппроксимирующего полинома. Дисперсия адекватности определяется с числом степеней свободы n_ад=N-(k+1).

Проверка гипотезы об адекватности состоит, по сути дела, в сопостав­лении дисперсии адекватности D _ад с оценкой дисперсии воспроизводимости отклика D_вос. Если эти оценки дисперсий однородны, то матема­тическое описание адекватно представляет результаты опыта, если же нет, то описание считается неадекватным. Проверку гипотезы об адекватности производят с использованием F -критерия Фишера, который характери­зуется отношением

F=D_ад/D_вос.

Если найденное эмпирически значение критерия F меньше критичес­кого F_кр, найденного из приложения 1 для соответствующих степеней свободы числителя v_ад = N - (k+l) и v_вос = q-1знаменателя при заданном уровне значимости a, то гипотезу об адекватности принимают. В противном случае гипотезу отвергают и математическое описание признается неадекватным.

Проверка адекватности возможна только при числе степеней свободы n_ад и n_вос больше нуля. Если число N вариантов варьирования плана ПФЭ равно числу оценок коэффициентов регрессии N = k + 1, то для проверки гипотезы об адекватности математического описания степеней свободы не остается (n_aд =0). Если же некоторые оценки коэффициен­тов регрессии оказались незначимыми, то число членов проверяемого уравнения в этом случае меньше числа N вариантов варьирования N > k + 1 и для проверки гипотезы об адекватности останется одна или несколько степеней свободы (n_ад > 0). Однако в этом случае необходи­мо исключить незначимые коэффициенты b_j из уравнения регрессии и пересчитать величину D _ад.

Если гипотеза об адекватности отвергается, необходимо переходить к более сложной форме математического описания либо, если это возмож­но, проводить эксперимент с меньшим интервалом варьирования D xj. Следует отметить, что максимальная величина интервала варьирования определяется условием адекватного описания объекта в области варьиро­вания. Если при больших интервалах варьирования математическая мо­дель неадекватна, то возникают систематические ошибки в определении коэффициентов, для уменьшения которых следует сузить область варьиро­вания. Однако с уменьшением интервала варьирования появляется целый рад новых трудностей: растет отношение помехи к полезному сигналу, что приводит к необходимости увеличения числа параллельных опытов для выделения полезного сигнала на фоне шума, иначе оценки коэффициентов могут стать статистически незначимыми.

Если линейная модель неадекватна, то необходимо оценить значи­мость влияния квадратичных членов уравнения (1.1) на выходную пере­менную. С этой целью используется статистика

,

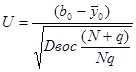подчиненная t - распределению Стьюдента с числом степеней свободы n_boc = q - 1.Если U < t_a, найденного из приложения 2 при заданном уровне значимости a, то влияние факторов хj² незначимо и им можно пренебречь. В противном случае нужно переходить к уравнению регрессии более высокого порядка.

Варианты задания области изменения факторов и значимых взаимо­действий представлены в табл. 1.3.

Таблица 1.3

Номер варианта	Границы области допустимых значений факторов	Значимые взаимодействия
Х1	Х2	Х3	Х4	Х5
	0;30	-10;40	0;70	-50;20	-15;15	x1x3, x1x4
	40;100	25;45	-10;80	20;100	25;65	x1x3, x1x5
	10;70	10;80	-15;65	50;90	40;100	x2x3, x3x4
	40;90	-20;20	10;60	50;100	-15;45	x1x4, x1x5
	20;60	0;60	-15;75	0;40	10;60	x1x4, x3x4
	10;60	-15;75	40;90	50;80	0;100	x1x3, x2x3
	45;85	40;120	30;100	20;70	50;120	x1x3, x3x4
	50;125	-20;50	20;80	40;90	30;80	x2x4, x2x5

Для проведения эксперимента и получения значений функции от­клика в заданных точках плана используется стандартная программа BLACKBOX, входящая в состав математического обеспечения кафед­ры. Способы обращения к программе и организации ввода данных представляются преподавателем.