1.2 Булевы функции
Основными объектами дискретной математики являются булевы функции. Предпосылкой их введения служат высказывания, которые составляют основную базу для построения теории булевых функций.
1.1 Логические операции.
Алгебра логики – самый простой раздел математической логики. Язык алгебры логики является одним из простейших языков математики. Основными объектами данного раздела являются высказывания. Понятие «высказывание» является первичным, оно не определяется, а поясняется. Под высказыванием понимают предложение, о котором можно сказать одно из двух: истинно оно или ложно. Например, высказывание «2 + 3 = 5» – истинное, высказывание «существует действительное число х такое, что
х 2 = –1» – ложное. Очевидно, не каждое предложение является высказыванием. Например, предложения: «Когда ты был дома?», «Пойдем со мной!» не являются высказываниями. Высказывания будем обозначать малыми латинскими буквами x, y, z,…, а их значения, т.е. истину и ложь, соответственно 1 и 0. Из двух данных высказываний с помощью связок «не», «и», «или», «если … то», «тогда и только тогда, когда …» можно образовать новые высказывания. Например, из высказываний «число 2 простое», «число 2 четное» с помощью указанных выше связок получаем высказывания: «число два простое и четное», «число 2 непростое», «число 2 простое или четное». Высказывание «если π иррационально, то π2 тоже иррационально» получается связыванием двух высказываний связкой «если … то». Эти операции соответствуют упомянутым выше связкам, употребляемым в обычной речи.
Рассмотрим примеры логических операций.
1 Логическая операция, соответствующая связке «и», называется конъюнкцией и обозначается &. В некоторых книгах эту операцию обозначают символом 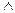 . Пусть x и y – высказывания. Высказывание x ×y назовем конъюнкцией x и y. Данное высказывание истинно тогда и только тогда, когда истинны оба высказывания x и y.
. Пусть x и y – высказывания. Высказывание x ×y назовем конъюнкцией x и y. Данное высказывание истинно тогда и только тогда, когда истинны оба высказывания x и y.
Соответствующее определение запишем в виде таблицы истинности:
| x | y | xy |
Определение конъюнкции двух высказываний естественным образом распространяется на любое конечное число высказываний.
Конъюнкция x1x2…xn, которую мы кратко обозначим через 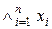 , истинна тогда и только тогда, когда истинны все высказывания.
, истинна тогда и только тогда, когда истинны все высказывания.
2 Логическая операция, соответствующая связке «или», называется дизъюнкцией и обозначается 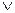 .
.
Пусть x и y – высказывания. Высказывание x Ú y назовем дизъюнкцией x и y. Данное высказывание истинно тогда и только тогда, когда хотя бы одно из высказываний x и y истинно.
Данное определение запишем в таблицы истинности:
| x | y | x 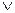 y y |
Определение дизъюнкции двух высказываний естественным образом распространяется на любое конечное число высказываний. Дизъюнкция x 1Ú x 2 Ú … Ú x n, которую мы кратко обозначим через 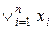 , истинна тогда и только тогда, когда хотя бы одно из высказываний x 1, x 2, …, x n истинно.
, истинна тогда и только тогда, когда хотя бы одно из высказываний x 1, x 2, …, x n истинно.
3 Логическая операция, соответствующая связке «не», называется отрицанием.
Отрицание высказывания x записывается так: 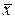 и определяется следующей таблицей истинности:
и определяется следующей таблицей истинности:
| x | 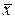 |
4 Логическая операция, соответствующая связке «если … то», называется импликацией. Эту операцию будем обозначать символом _. При этом высказывание «если x, то y» записывается в виде x _ y. Высказывание x называется посылкой импликации, y – ее заключением. Импликация двух высказываний x и y задается следующей таблицей истинности:
| x | y | x _ y |
Из определения импликации вытекает, что:
· импликация с ложной посылкой всегда истинна;
· импликация с истинным заключением всегда истинна;
· импликация ложна тогда и только тогда, когда посылка истинна, а заключение ложно.
5 Логическая операция, соответствующая связке «тогда и только тогда, когда …» называется эквивалентностью и обозначается символом n.
Пусть x и y – высказывания. Высказывание x n y назовем эквивалентностью x и y. Данное высказывание истинно тогда и только тогда, когда оба
высказывания x и y или истинны или ложны.
Данное определение запишем в виде таблицы истинности:
| x | y | x n y |
 2014-09-02
2014-09-02 1105
1105








