Пусть задано отображение 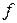 :
: 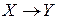 и пусть множество
и пусть множество 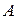 является подмножеством множества
является подмножеством множества 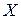 , т.е.
, т.е. 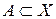 . Обозначим через
. Обозначим через 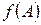 подмножество множества
подмножество множества 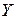 , образованное из всех элементов
, образованное из всех элементов 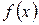 , где
, где 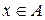 , т.е.
, т.е.
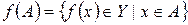 .
.
Определение 1. Подмножество 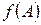 называется образом подмножества
называется образом подмножества 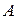 при отображении
при отображении 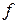 .
.
Определение 2. Совокупность всех тех элементов 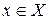 , образом которых является данный элемент
, образом которых является данный элемент 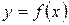 ,
, 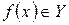 , называется прообразом элемента
, называется прообразом элемента 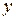 при отображении
при отображении 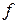 и обозначается
и обозначается 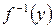
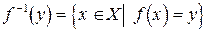 .
.
Очевидно, если 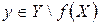 , то
, то 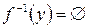 . Например, пусть
. Например, пусть 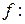
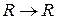 , где
, где 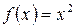 , тогда
, тогда 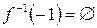 .
.
Определение 3. Пусть множество 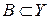 . Прообразом множества
. Прообразом множества  при отображении
при отображении 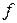 называется множество элементов
называется множество элементов 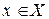 , таких, что
, таких, что 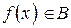 и обозначается
и обозначается 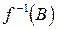 :
:
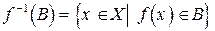 .
.
Очевидно, что 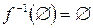 .
.
Примеры.
1. 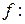
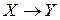
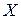
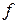
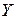
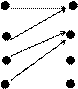

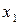
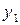
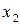
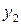
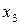
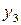
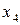
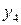
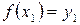
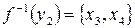
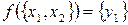
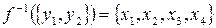
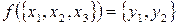
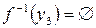
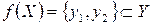
2. 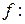
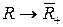 ,
, 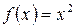
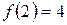 ,
, 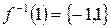
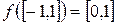 ,
, 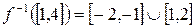
3. Функция задана с помощью таблицы:
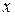 | -1 | |||
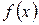 |
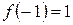 ,
, 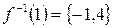
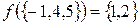 ,
, 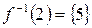 ,
, 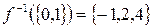 .
.
 2015-01-21
2015-01-21 14510
14510
