Лекция 3 Преобразование Фурье

3.1. Преобразование Фурье функций из пространства L ₁(R)

3.2. Преобразование Фурье в пространстве L ₂(R)

3.1. Преобразование Фурье функций из пространства L₁(R)

Преобразованием Фурье функции f, заданной на прямой R, называется функция 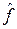, определенная формулой

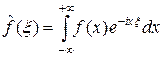. (1)

Теорема 3.1. Если функция f Î L ₁(R), то ее преобразование Фурье определено, удовлетворяет неравенству

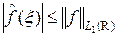(2)

и является непрерывной функцией на R, причем .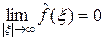

Доказательство. Так как 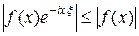, то из свойств интеграла Лебега получаем

,

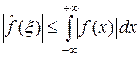т. е. неравенство (2). Значит, преобразование Фурье 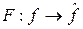можем рассматривать как отображение из пространства L ₁(R) в пространство ограниченных функций и, согласно неравенству (2), это отображение ограничено. Линейность отображения F очевидна.

Пусть j (x) – характеристическая функция интервала (a, b).Тогда

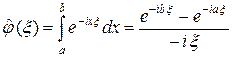(3)

и, значит, 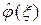– непрерывная на R функция и 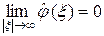. Аналогично доказательству теоремы 11.2 курса «Функциональный анализ. Часть 1» получаем, что линейные комбинации характеристических функций интервалов плотны в пространстве L ₁(R), их образы являются линейными комбинациями функций вида (3) и, следовательно, непрерывными функциями, стремящимися к нулю на бесконечности.

Пусть теперь f – произвольная функция из L ₁(R) и пусть f_n – последовательность ступенчатых функций (т. е. линейных комбинаций характеристических функций интервалов) такая, что 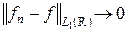. Тогда в силу неравенства (2) последовательность 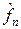равномерно сходится к функции 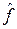и, значит, функция 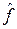как предел равномерно сходящейся последовательности непрерывных функций является функцией непрерывной. Свойство 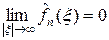также сохраняется при равномерной сходимости. В самом деле, возьмем e > 0 и выберем номер n ₀ так, чтобы выполнялось 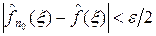и число M так, что при | x | > M будет 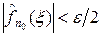. Тогда для x таких, что | x | > M, получаем 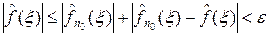. Теорема доказана.

Замечание 3.1. Не любая функция, непрерывная на R и стремящаяся к нулю на бесконечности, является преобразованием Фурье функции из L ₁(R). Можно показать, например, что функция

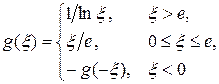
не является преобразованием Фурье функции из L ₁(R), хотя она непрерывна и .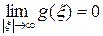

Заметим также, что функция 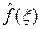может быть неинтегрируемой (например, функция 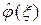из формулы (3)).

Возникает задача: как по образу 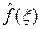найти исходную функцию f (x). Поскольку для элементов f из пространства L ₁(R) значение в точке, вообще говоря, не определено, то естественно ожидать, что значение f (x) в точке x можно найти лишь для функций, удовлетворяющих дополнительным условиям.

Определение 3.1. Функция f удовлетворяет в точке x ₀ условию Дини, если функция

j (x) = [ f (x ₀ + t) – f (x ₀) ] / t

интегрируема в некоторой окрестности точки t = 0.

Условию Дини удовлетворяет, например, абсолютно непрерывная функция, имеющая ограниченную производную. Действительно, если | f ¢ (x) | £ M, то

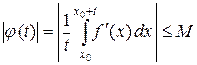
и, значит, условие Дини выполнено.

Теорема 3.2. Если функция f Î L ₁(R) и в некоторой точке x удовлетворяет условию Дини, то в этой точке справедливо равенство

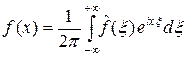, (4)

причем интеграл в (4) есть интеграл в смысле главного значения.

Доказательство. Рассмотрим функцию

.

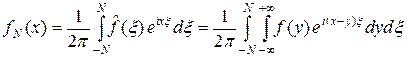Так как существует повторный интеграл

,

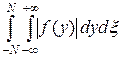то по теореме Фубини можем изменить порядок интегрирования и, учитывая, что

,

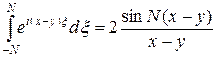получаем

.

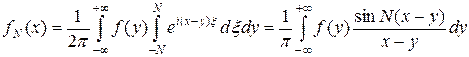Сделав замену переменной t = x – y, получаем

.

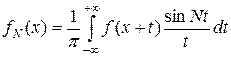Из курса математического анализа известно, что при N > 0 справедливо равенство

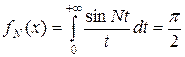, (5)

причем несобственный интеграл сходится условно и равномерно по N при N ³ 1, подынтегральная функция не интегрируема по Лебегу. Представляя f (x) в виде

,

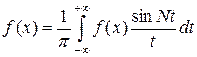получаем

.

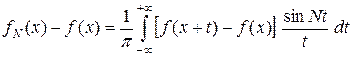Покажем, что последний интеграл стремится к нулю при N → ¥. Возьмем e > 0 и в силу равномерной сходимости интеграла (5) выберем число A > 0 так, чтобы

.

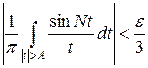Тогда разность представима в виде

.

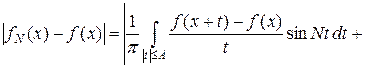
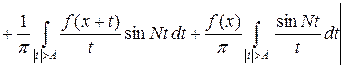При | t | > 1 имеем (sin N t) / t < 1. Поэтому, выбрав достаточно большим число A, получим, что

.

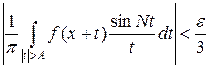По условию Дини функция

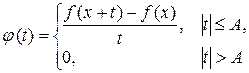
интегрируема, и по теореме 3.1 получаем, что

.

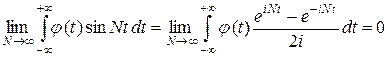Значит, существует число N ₀ такое, что при N > N ₀ выполнено

.

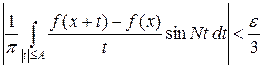Тогда при N > N ₀ будем иметь 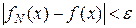. Это означает, что

.

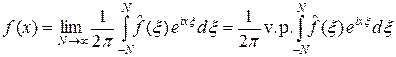Теорема доказана.

Определение 3.2. Пусть X – произвольное множество, S – s -кольцо его подмножеств. Отображение F: S → R называется зарядом (или знакопеременной мерой), если оно s -аддитивно, т. е. из разложения 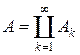, , 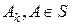следует, что .

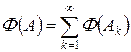Из определения 3.2 следует, что последний ряд сходится абсолютно, так как его сумма не зависит от способа нумерации множеств A_k.

Определение 3.3. Измеримое множество A Ì X называется положительным (отрицательным) относительно заряда F, если для любого измеримого подмножества B Ì A, F (B) ³ 0 (F (B) £ 0).

Лемма 3.1. Если заряд F задан на s -кольце S подмножеств из X, то 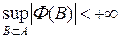для любого A Ì S.

Доказательство. Обозначим 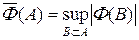. Предположим, что для некоторого множества A Î S имеем 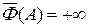. Покажем, что существует последовательность A É A ₁ É A ₂ É ¼ такая, что | F (A_n)| > n. Выберем B ₁ Ì A так, что | F (B ₁)| > | F (A)| + 1. Тогда для A \ B ₁ имеем | F (A \ B ₁)| = | F (A) –
– F (B ₁)| ³ | F (B ₁)| – | F (A)| > 1. Положим

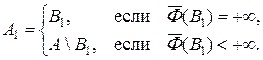
Тогда | F (A ₁)| = +¥. Далее построение ведем по индукции. В множестве A_{n – 1} выбираем подмножество B так, что | F (B_n)| > | F (A_{n – 1})| + n, и полагаем

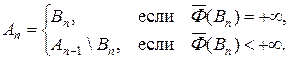
Тогда в силу s -аддитивности заряда существует конечный предел 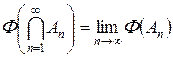. Но, с другой стороны, | F (A_n)| → ¥. Полученное противоречие доказывает лемму.

Лемма 3.2. Пусть F – заряд, заданный на s -кольце S подмножеств из X. Тогда существует такое положительное подмножество X ⁺ Ì X и отрицательное подмножество X ^– Ì X, что X = X ⁺ C X ^–.

Доказательство. Покажем сначала, что если F (A) < 0, то в A существует отрицательное множество A ₀. Если само A отрицательно, то утверждение очевидно. Если же A не отрицательно, то в A существуют множества с положительным зарядом. Выбираем среди них такое B ₁, что F (B ₁) > S F (A) –
– 1/2, где .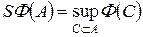

Положим A ₁ = A \ B ₁. Далее, по индукции строим множество B_n Ì A_{n – 1} такое, что F (B_n) ³ S F (A_{n – 1}) – 1/2 ⁿ, и полагаем A_n = A_{n – 1} \ B_n. Так как F (B_n) > 0, то F (A_n) < F (A_{n – 1}) < F (A) < 0. Пусть 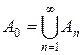. Тогда 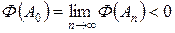. Покажем, что A ₀ – отрицательное множество. Предположим, что существует подмножество B Ì A ₀ такое, что F (B) > 0. Выберем номер n так, чтобы 1/2 ⁿ < F (B). Тогда

F (B È B_n) = F (B) + F (B_n) > S F (A_{n – 1})

(B Ì A_n, B_n Ë A_n, (B È B_n) Ì A_{n – 1}),

что противоречит определению множества S F (A_{n – 1}).

Перейдем к построению множеств X ⁺ и X ^–. Пусть b = inf F (A), где нижняя грань вычисляется по всем отрицательным подмножествам из X. Пусть A_n – последовательность отрицательных подмножеств такая, что 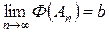, и пусть 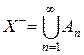. Множество X ^– отрицательно и F (X ^–) = b.

Покажем, что множество X ⁺ = X \ X ^– положительно. Если в X ⁺ существует A такое, что F (A) < 0, то по доказанному существует отрицательное множество A ₀ Ì A и F (A ₀) < 0. Тогда X ^– C A ₀ – отрицательное множество, причем F (X ^– C A ₀) = F (X ^–) + F (A ₀) < b, что противоречит определению числа b. Значит, X ⁺ – положительное множество. Лемма доказана.

Лемма 3.3. Для любого заряда F существуют взаимно сингулярные меры m ₁ и m ₂ такие, что F (A) = m ₁(A) – m ₂(A) (см. определение 4.4 курса «Функциональный анализ. Часть 1»).

Доказательство. Положив m ₁(A) = F (X ⁺ I A) и m ₂(A) = – F (X ^– I A), получим требуемое разложение.

Рассмотрим подробнее заряды на s -алгебре, порожденной полуинтервалами на отрезке [0, 1]. Каждому заряду n (как и мере) на этой s -алгебре поставим в соответствие функцию F ²(t) = n ([0, t)), F ²(0) = 0. Опишем класс функций на [0, 1], которые соответствуют зарядам. Лемма доказана.

Пусть S – s -алгебра подмножеств множества X и m – мера на S.

Определение 3.4. Заряд n называется абсолютно непрерывным относительно меры m, если из m (A) = 0 следует n (A) = 0.

Например, абсолютно непрерывным является заряд n, заданный формулой

.

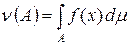Лемма 3.4. Пусть ненулевая мера n абсолютно непрерывна относительно меры m. Тогда существует m -измеримое множество B и d > 0 такие, что m (B) > 0 и для любого A Ì B

n (A) ³ d m (A) (6)

Доказательство. Неравенство (6) означает, что множество B положительно относительно заряда F = n – d m. Рассмотрим последовательность зарядов F _n = n – m / n. Пусть 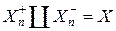– разложение X на положительное и отрицательное множества для заряда F _n. Для подмножества 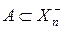справедливо неравенство

n (A) £ m (A) / n. (7)

Если 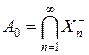, то (7) справедливо с любым n, т. е. n (A ₀) = 0. Поэтому n (X \ A ₀) > 0. Ввиду абсолютной непрерывности n относительно m имеем m (X \ A ₀) > 0. Так как 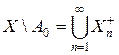, то существует n ₀ такое, что 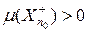. Полагая 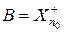и d = 1 / n ₀, получаем утверждение леммы. Лемма доказана.

Лемма 3.5(И. Радон, О. Никодим). Если заряд n абсолютно непрерывен относительно меры m, то существует m -интегрируемая функция f такая, что 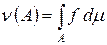для любого A Î S.

Доказательство. Согласно лемме 3.3, заряд может быть представлен в виде разности двух мер m ₁ и m ₂, причем если заряд n абсолютно непрерывен относительно меры m, то и меры m ₁ и m ₂ также абсолютно непрерывны относительно m. Поэтому доказательство проведем для мер. Обозначим через H следующее множество функций:

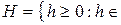L₁(Х, m), .

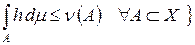Пусть 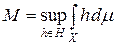. Возьмем последовательность h_n Î H такую, что 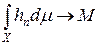. Построим новую последовательность f_n = max{ h ₁,¼, h_n }. Тогда f_n (x) £ f_{n + 1} (x). Положим A_k = { x Î A : f_n (x) = h_k (x), f_n (x) ¹ h_i (x), i = 1,¼, k – 1}. Тогда 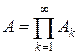и

.

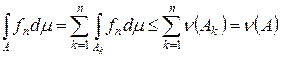Значит, f_n Î H и по теореме Б. Леви (теорема 6.4 курса «Функциональный анализ. Часть 1») f_n сходится к интегрируемой функции f и 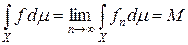. Кроме того, 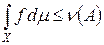. Следовательно, f Î H. Это означает, что 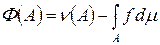– мера. Нам нужно доказать, что F (A) = 0 для любого A Ì X. Для этого достаточно показать, что F (X) = 0. Предположим противное, т. е. F (X) > 0. Тогда по лемме 3.4 найдутся множество B Ì X и число d > 0 такие, что F (A) > d m (A) для любого A Ì B и m (B) > 0. Возьмем функцию h ₀ (x) = d c_B (x). Тогда

,

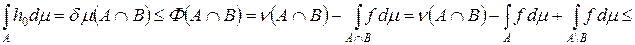
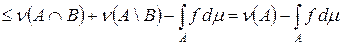т. e. 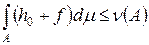. Следовательно, h ₀ + f Î H и 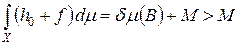, что противоречит определению числа M. Таким образом, F (X) = 0. Теорема доказана.

Пусть F – заряд на [0, 1], заданный с помощью функции g (t). Заряд F абсолютно непрерывен относительно меры Лебега тогда и только тогда, когда функция g (t) абсолютно непрерывна (теорема 4.3 курса «Функциональный анализ. Часть 1»). По лемме 3.5 существует такая интегрируемая функция f, что 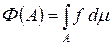. В частности, если A = [ a, b ] Ì [0, 1], то

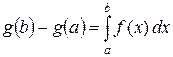. (8)

Если функция g непрерывно дифференцируема, то f – производная и формула (8) является формулой Ньютона – Лейбница. Если функцию f назвать обобщенной производной абсолютно непрерывной функции g, то (8) представляет собой обобщение формулы Ньютона – Лейбница. Можно доказать, что абсолютно непрерывная функция g имеет почти всюду обычную производную и эта производная почти всюду совпадает с f.

Заметим, что если функция g не является абсолютно непрерывной, то не существует интегрируемой функции f, при которой формула (8) имеет место для любых a и b. Действительно, правая часть равенства определяет заряд, абсолютно непрерывный относительно меры Лебега, а левая – заряд, не являющийся абсолютно непрерывным. В частности, даже если функция g непрерывна и почти всюду имеет производную g', но не является абсолютно непрерывной, то формула Ньютона – Лейбница не выполняется. Примером может служить функция Кантора j (t). Эта функция непрерывна и j ' (t) = 0 почти всюду (на дополнении к канторову множеству). Но .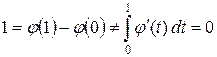

Если мера n абсолютно непрерывна относительно меры m, то функцию f такую, что 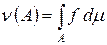, называют (по аналогин с предыдущим примером) производной Радона – Никодима меры n по мере m и она обозначается dn / dm.

Рассмотрим основные свойства преобразования Фурье.

1^°. Если функция f интегрируема и абсолютно непрерывна, а ее обобщенная производная f ¢ интегрируема, то .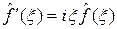

Доказательство. Как показано выше, для функции f справедлива формула Ньютона – Лейбница

.

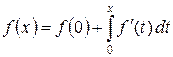Поэтому существует предел

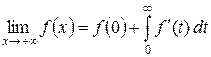
и 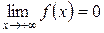, так как функция f интегрируема. Аналогично получаем .

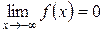Тогда интегрированием по частям получаем

.

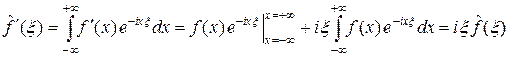Свойство доказано.

2^°. Если f Î L ₁(R) и x f (x) Î L ₁(R), то функция 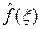непрерывно дифференцируема и

.

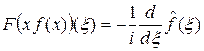Доказательство. Рассмотрим приращение

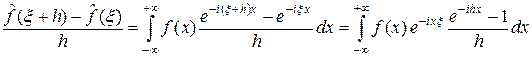. (9)

Так как 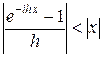, подынтегральные функции в (9) мажорируются интегрируемой функцией | x f (x) | и, значит, по теореме Лебега можно перейти к пределу при h ® 0. Получаем

.

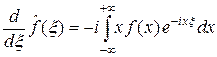Свойство доказано.

3^°. Сверткой функций f и g называется функция 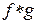, определенная формулой

.

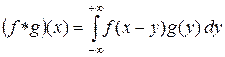Если функции f и g принадлежат L ₁(R), то их свертка 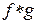определена почти всюду и принадлежит L ₁(R). При этом 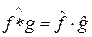, т. е. при преобразовании Фурье свертка переходит в обычное произведение функций.

Доказательство. Рассмотрим повторный интеграл

.

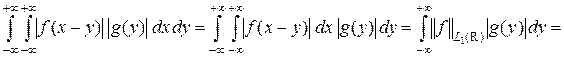
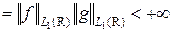По теореме Фубини существует двойной интеграл и существует повторный интеграл, полученный переменой порядка интегрирования:

.

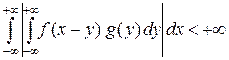Существование этого интеграла означает, что свертка 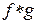определена почти всюду и является интегрируемой функцией. Тогда

.

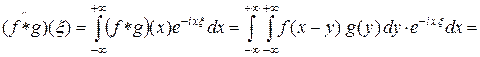
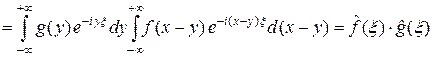Свойство доказано.

4^°. Пусть f Î L ₁(R), h Î R, g (x) = f (x + h) и j (x) = e ^{i x h}f (x). Тогда , .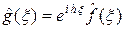

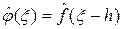Доказательство. Имеем

,

.

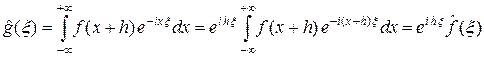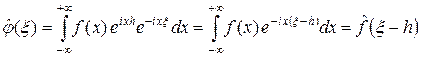Свойство доказано.

3.2. Преобразование Фурье в пространстве L₂(R)

Если функция f принадлежит пространству L ₂(R), то интеграл в формуле (1), задающей преобразование Фурье, может оказаться расходящимся. Покажем, что для функций из L ₂(R) преобразование Фурье можно задать иначе. Основой для этого задания является следующее утверждение.

Теорема 3.3. Если функция f дважды непрерывно дифференцируема и f, f ' и f " принадлежат L ₁(R), то справедливо равенство Парсеваля

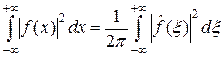. (10)

Доказательство. Согласно свойству 1 преобразования Фурье в L ₁(R), функция x ² f (x) является преобразованием Фурье функции f " (x) и по теореме 3.1 ограничена некоторой постоянной M. Тогда 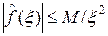, откуда следует, что функция f интегрируема. Функция f удовлетворяет условию Дини, для нее справедлива формула обратного преобразования Фурье и, так как функция f интегрируема, интеграл в формуле (4) можно рассматривать как обычный несобственный интеграл, а не интеграл в смысле главного значения.

Так как функция f ограничена и интегрируема, то произведение 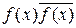является интегрируемой функцией и получаем

.

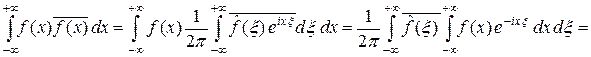
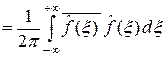Изменение порядка интегрирования допустимо в силу теоремы Фубини, так как функция 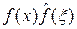интегрируема. Теорема доказана.

Функции f, удовлетворяющие условию теоремы 3.3, образуют всюду плотное множество в L ₂(R). Оператор F преобразования Фурье, определенный на этих функциях, является ограниченным в норме L ₂(R) и, более того, равенство Парсеваля означает, что

.

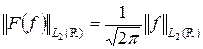По непрерывности этот оператор может быть продолжен на все пространство L ₂(R) до оператора, который будем обозначать той же буквой F. При этом в силу теоремы о продолжении равенство Парсеваля (10) будет выполняться для продолженного оператора и, в частности, все образы F ( f ) принадлежат L ₂(R). Обратное преобразование Фурье также продолжается на все пространство L ₂(R), и это продолжение является обратным к преобразованию F в силу теоремы о продолжении (теорема 10.7 курса «Функциональный анализ. Часть 1»).

Продолжение по непрерывности в данном случае может быть описано следующим образом. Пусть f Î L ₂(R). Тогда функция

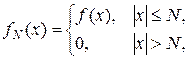
является интегрируемой и 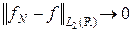. Для функции f_N существует обычное преобразование Фурье, коюрое совпадает с преобразованием, определенным как продолжение по непрерывности. В силу равенства Парсеваля получаем

,

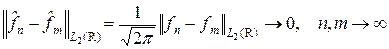т. е. последовательность 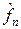является последовательностью Коши в L ₂(R). В силу полноты этого пространства 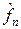сходится к некоторой функции 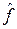, которая по определению является преобразованием Фурье функции f. Таким образом, для f из L ₂(R) получаем

,

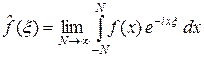причем предел понимается в смысле сходимости в L ₂(R). Таким образом, пространство L ₂(R) при преобразовании Фурье биективно отображается па L ₂(R) и поэтому применение преобразования Фурье в пространстве L ₂(R) оказывается наиболее эффективным. Преобразование Фурье в пространстве L ₂(R) обладает свойствами 1) – 4) из раздела 3.1.