Магнитная постоянная. Единицы магнитной индукции и напряженности магнитного поля

Если два параллельных проводника с током находятся в вакууме (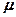 = 1), то сила взаимодействия на единицу длины проводника, согласно (111.5), равна

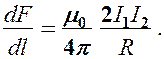(112.1)

Для нахождения числового значения 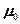воспользуемся определением ампера, согласно которому при 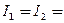1A и R = 1м 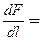2×10^-7 Н/м. Подставив это значение в формулу (112.1), получим 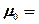4p10^-7 Н/А² = 4p10^-7 Гн/м, где генри (Гн) — единица индуктивности (см. § 126).

Закон Ампера позволяет определить единицу магнитной индукции В. Предположим, что элемент проводника dl с током I перпендикулярен направлению магнитного поля. Тогда закон Ампера (см. (111.2)) запишется в виде dF = IBdl, откуда

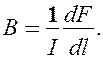
Единица магнитной индукции — тесла (Тл): 1 Тл — магнитная индукция такого однородного магнитного поля, которое действует с силой в 1Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику проходит ток в 1А: 1Тл = 1Н/(А×м).

Так как 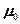= 4×10^-7 Н/А², а в случае вакуума ( 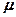= 1), согласно (109.3), В = 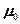H, то для данного случая

Единица напряженности магнитного поля — ампер на метр (А/м): 1А/м — напряженность такого поля, магнитная индукция которого в вакууме равна 4л×10^-7 Тл.