| 
| 
|
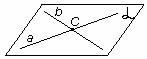
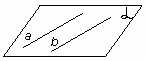
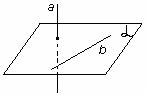
| рис. 14. Пересекающиеся прямые (лежат в одной плоскости). | рис. 15. Параллельные прямые (лежат в одной плоскости). | рис. 16. Скрещивающиеся прямые (не лежат в одной плоскости). |
Замечания:
1.
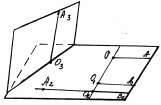 рис. 17 рис. 17
| лучи ОА и О1А1 сонаправлены лучи А2В2 и О2В2 сонаправлены лучи О3А3 и О1А1 не являются сонаправленными |
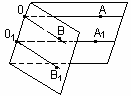 рис. 18 рис. 18
| ОА || О1А1 ОВ || О1 В1, то угол АОВ равен углу А1О1В1 (углы с сонаправленными сторонами) |
2. Угол между прямыми.
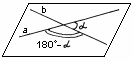 рис. 19 рис. 19
| Если  - меньший из всех образованных углов, то угол (a; b) = - меньший из всех образованных углов, то угол (a; b) = 
|
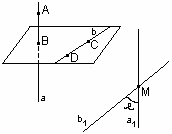 рис. 20 рис. 20
| а и b - скрещивающиеся прямые. М - произвольная точка пространства, через которую проведём прямые а1||а и b1||b Если угол (а1; b1) = 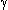 , то угол (а;b) = , то угол (а;b) = 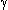
|
8. Плоскости могут совпадать, быть параллельными или пересекаться по прямой.
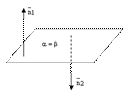
рис.3.
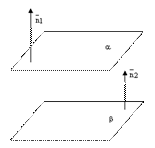

рис.4.
рис.5.
Теорема. Пусть
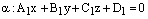 и
и 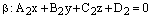
– общие уравнения двух плоскостей. Тогда:
1) если 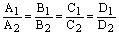 , то плоскости совпадают;
, то плоскости совпадают;
2) если 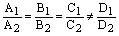 , то плоскости параллельны;
, то плоскости параллельны;
3) если 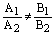 или
или 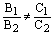 , то плоскости пересекаются и система уравнений
, то плоскости пересекаются и система уравнений
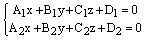 (6)
(6)
является уравнениями прямой пересечения данных плоскостей.
Доказательство. Первое и второе условия теоремы равносильны коллинеарности нормальных векторов данных плоскостей:
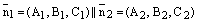 .
.
Если 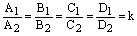 , то
, то 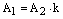 ,
, 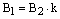 ,
, 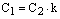 ,
, 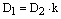 и уравнение плоскости
и уравнение плоскости 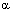 принимает вид:
принимает вид:
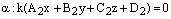
Коэффициент пропорциональности k не может быть равен нулю, т.к. 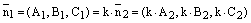 и при
и при 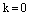 получаем, что
получаем, что 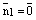 , что противоречит определению нормального вектора. Следовательно, уравнение плоскости
, что противоречит определению нормального вектора. Следовательно, уравнение плоскости 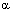
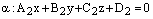
совпадает с уравнением плоскости 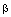 , а это означает, что плоскости совпадают.
, а это означает, что плоскости совпадают.
Если 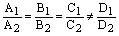 , то это означает коллинеарность нормальных векторов обеих плоскостей, а значит плоскости либо параллельны, либо совпадают. Но в этом случае плоскости не могут совпадать и остается единственная возможность их параллельности.
, то это означает коллинеарность нормальных векторов обеих плоскостей, а значит плоскости либо параллельны, либо совпадают. Но в этом случае плоскости не могут совпадать и остается единственная возможность их параллельности.
Третье условие теоремы равносильно тому, что нормальные векторы плоскостей не коллинеарные, а потому они не совпадают и не параллельны, а следовательно, они пересекаются. Из геометрии известно, что линия пересечения двух плоскостей является прямой.
Точка М лежит на прямой пересечения двух плоскостей 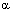 и
и 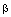 тогда и только тогда, когда она лежит одновременно на обеих плоскостях и ее координаты удовлетворяют обоим уравнениям системы (6), т.е. являются решением этой системы. А это означает, что система (6) является уравнениями прямой пересечения плоскостей, ч.т.д.
тогда и только тогда, когда она лежит одновременно на обеих плоскостях и ее координаты удовлетворяют обоим уравнениям системы (6), т.е. являются решением этой системы. А это означает, что система (6) является уравнениями прямой пересечения плоскостей, ч.т.д.
Теорема доказана.
 2015-01-21
2015-01-21 492
492








