Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.


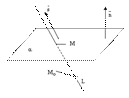
рис.6.
рис.7.
рис.8.
Теорема. Пусть плоскость 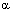 задана общим уравнением
задана общим уравнением
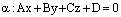 ,
,
а прямая L задана каноническими уравнениями
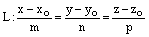
или параметрическими уравнениями
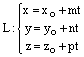 ,
, 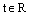 ,
,
в которых 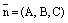 – координаты нормального вектора плоскости
– координаты нормального вектора плоскости 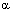 ,
, 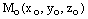 – координаты произвольной фиксированной точки прямой L,
– координаты произвольной фиксированной точки прямой L, 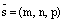 –
–
координаты направляющего вектора прямой L. Тогда:
1) если 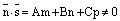 , то прямая L пересекает плоскость
, то прямая L пересекает плоскость 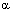 в точке, координаты которой
в точке, координаты которой 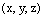 можно найти из системы уравнений
можно найти из системы уравнений
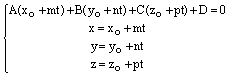 ; (7)
; (7)
2) если 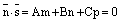 и
и 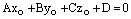 , то прямая лежит на плоскости;
, то прямая лежит на плоскости;
3) если 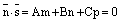 и
и 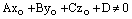 , то прямая параллельна плоскости.
, то прямая параллельна плоскости.
Доказательство. Условие 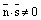 говорит о том, что вектроры
говорит о том, что вектроры 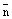 и
и 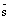 не ортогональны, а значит прямая не параллельна плоскости и не лежит в плоскости, а значит пересекает ее в некоторой точке М. Координаты точки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальные уравнения системы, находим координаты искомой точки.
не ортогональны, а значит прямая не параллельна плоскости и не лежит в плоскости, а значит пересекает ее в некоторой точке М. Координаты точки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальные уравнения системы, находим координаты искомой точки.
Если 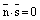 , то это означает, что
, то это означает, что 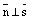 . А такое возможно лишь тогда, когда прямая лежит на плоскости или параллельна ей. Если прямая лежит на плоскости, то любая точка прямой является точкой плоскости и координаты любой точки прямой удовлетворяют уравнению плоскости. Поэтому достаточно проверить, лежит ли на плоскости точка
. А такое возможно лишь тогда, когда прямая лежит на плоскости или параллельна ей. Если прямая лежит на плоскости, то любая точка прямой является точкой плоскости и координаты любой точки прямой удовлетворяют уравнению плоскости. Поэтому достаточно проверить, лежит ли на плоскости точка 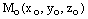 . Если
. Если 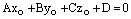 , то точка
, то точка  – лежит на плоскости, а это означает, что и сама прямая лежит на плоскости.
– лежит на плоскости, а это означает, что и сама прямая лежит на плоскости.
Если 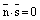 , а
, а 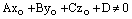 , то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.
, то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.
Теорема доказана.
9. Плоскость, прямая, точка — основные понятия геометрии. Нам трудно дать им четкие определения, однако интуитивно мы понимаем, что это такое. Плоскость имеет только два измерения. У нее нет глубины. Прямая имеет лишь одно измерение, а у точки вообще нет размеров — ни длины, ни ширины, ни высоты.
10. Два вектора всегда являются компланарными так же, как три точки всегда лежат в одной плоскости. Но три вектора уже могут не быть компланарными, и тогда любой из них не может быть выражен через два других. Но, если мы выберем в пространстве три некомпланарных базисных вектора, то любой четвертый уже может быть выражен через них в виде линейной комбинации.
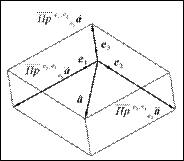
Рис. 13
Поступая аналогично тому, как мы это сделали для "плоского" случая, спроектируем вектор 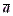 на базисные векторы
на базисные векторы 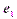 ,
, 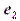 и
и 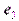 при помощи проектирующих плоскостей (
при помощи проектирующих плоскостей (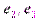 ), (
), (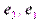 ) и (
) и (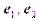 ) (рис. 13). Выразив каждую из проекций через соответствующий вектор базиса, получим:
) (рис. 13). Выразив каждую из проекций через соответствующий вектор базиса, получим:
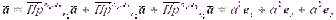 .
.
То же самое в сокращенной записи:
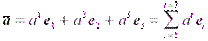 .
.
11. Два геометрических вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Доказательство. Необходимость. Пусть векторы 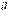 и
и 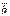 линейно зависимы, следовательно,
линейно зависимы, следовательно, 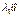 +
+ 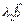 =
= 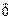 , причем хотя бы одно из чисел l 1, l 2 отлично от 0. Допустим для определенности l 2¹0. Тогда
, причем хотя бы одно из чисел l 1, l 2 отлично от 0. Допустим для определенности l 2¹0. Тогда
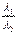
 +
+  =
= 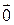 ,
,  =
= 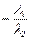
 ,
,
т. е. векторы  и
и  коллинеарны.
коллинеарны.
Достаточность. Пусть векторы  и
и  коллинеарны. Будем считать, что среди них нет нулевого вектора, ибо в противном случае в силу теоремы 3.3.2 эти векторы будут линейно зависимы.
коллинеарны. Будем считать, что среди них нет нулевого вектора, ибо в противном случае в силу теоремы 3.3.2 эти векторы будут линейно зависимы.
Если ненулевые векторы  и
и  коллинеарны, то в соответствии с теоремой 3.1.2 вектор
коллинеарны, то в соответствии с теоремой 3.1.2 вектор  представим в виде
представим в виде  =
= 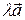 . Тогда
. Тогда 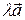 +(– 1)
+(– 1)  =
= 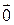 , что и означает линейную зависимость векторов
, что и означает линейную зависимость векторов  и
и  .
.
Следствие 3. 4.1. Любые два неколлинеарных вектора  и
и  являются линейно независимыми.
являются линейно независимыми.
Теорема 3.4.2. Три вектора в линейном пространстве V 3 являются линейно зависимыми тогда и только тогда, когда они компланарны.
Доказательство. Необходимость. Пусть векторы  ,
,  ,
, 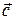 линейно зависимы, следовательно, существуют такие вещественные числа a, b, d, что
линейно зависимы, следовательно, существуют такие вещественные числа a, b, d, что 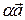 +
+ 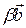 +
+ 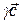 =
= 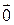 , при этом хотя бы одно из них не равно нулю. Допустим для определенности, что g ¹ 0. Тогда
, при этом хотя бы одно из них не равно нулю. Допустим для определенности, что g ¹ 0. Тогда
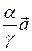 +
+ 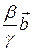 +
+ 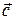 =
= 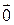
или
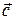 =
= 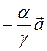
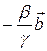 .
.
Векторы 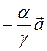 ,
, 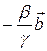 коллинеарны соответственно векторам
коллинеарны соответственно векторам  и
и  , а их сумма, т. е. вектор
, а их сумма, т. е. вектор 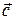 , будет лежать в плоскости векторов
, будет лежать в плоскости векторов  и
и  . Следовательно, векторы
. Следовательно, векторы  ,
,  ,
, 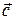 компланарны.
компланарны.
Достаточность. Пусть векторы  ,
,  ,
, 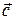 компланарны. Будем считать, что среди них нет ни одной пары коллинеарных, ибо в противном случае в силу теоремы 3.3.3 три данных вектора будут линейно зависимыми.
компланарны. Будем считать, что среди них нет ни одной пары коллинеарных, ибо в противном случае в силу теоремы 3.3.3 три данных вектора будут линейно зависимыми.
 Приведем векторы
Приведем векторы  ,
,  ,
, 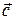 к общему началу О (рис. 3.4.1). Проведем через точку С прямую С
к общему началу О (рис. 3.4.1). Проведем через точку С прямую С  , параллельную вектору
, параллельную вектору  и пересекающую прямую О
и пересекающую прямую О  в точке В. Далее параллельно вектору
в точке В. Далее параллельно вектору  спроектируем точку С на прямую О
спроектируем точку С на прямую О  . Векторы
. Векторы 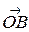 и
и  , а также
, а также 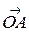 и
и  коллинеарны. Тогда в силу теоремы 3.1.2
коллинеарны. Тогда в силу теоремы 3.1.2 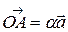 ,
, 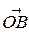 =
= 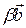 . Однако
. Однако 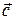 =
= 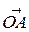 +
+ 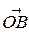 =
= 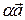 +
+ 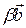 , откуда
, откуда 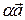 +
+ 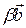 + (–1)
+ (–1) 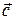 =
= 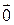 , что и означает линейную зависимость векторов
, что и означает линейную зависимость векторов  ,
,  ,
, 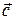 .
.
Следствие 3. 4.2. Если векторы  ,
,  ,
, 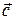 некомпланарны, то они линейно независимы в V 3.
некомпланарны, то они линейно независимы в V 3.
Следствие 3. 4.3. Каковы бы ни были два неколлинеарных вектора  ,
,  на плоскости, всякий третий вектор
на плоскости, всякий третий вектор 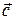 , лежащий в этой же плоскости, может быть разложен по векторам
, лежащий в этой же плоскости, может быть разложен по векторам  и
и  в виде
в виде 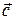 =
= 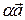 +
+ 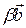 .
.
Теорема 3.4.3. Любые четыре вектора линейного пространства V 3 линейно зависимы.
Доказательство. Пусть  ,
,  ,
, 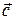 ,
, 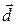 — произвольные векторы в пространстве V 3. Будем считать, что среди этих векторов никакие три не являются компланарными, ибо в противном случае данные четыре вектора будут заведомо линейно зависимы.
— произвольные векторы в пространстве V 3. Будем считать, что среди этих векторов никакие три не являются компланарными, ибо в противном случае данные четыре вектора будут заведомо линейно зависимы.
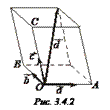 Приведем все векторы к общему началу О (рис. 3.4.2). Проведем через конец вектора
Приведем все векторы к общему началу О (рис. 3.4.2). Проведем через конец вектора  плоскости параллельные плоскостям, в которых лежат пары векторов
плоскости параллельные плоскостям, в которых лежат пары векторов  и
и  ,
,  и
и 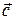 ,
,  и
и  соответственно. Обозначим через A, B, C соответственно точки пересечения указанных плоскостей с прямыми О
соответственно. Обозначим через A, B, C соответственно точки пересечения указанных плоскостей с прямыми О  ,
,
О  , О
, О 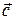 .
.
Векторы 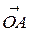 и
и  ,
, 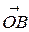 и
и  ,
, 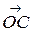 и
и 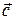 коллинеарны. Поэтому по теореме 3.1.2
коллинеарны. Поэтому по теореме 3.1.2 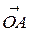 =
= 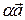 ,
, 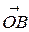 =
= 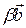 ,
, 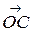 =
= 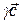 . Однако
. Однако 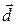 =
= 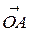 +
+ 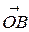 +
+ 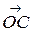 , откуда
, откуда 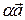 +
+ 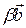 +
+ 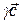 + (– 1)
+ (– 1) 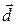 =
= 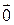 , что и означает линейную зависимость векторов
, что и означает линейную зависимость векторов  ,
,  ,
, 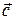 ,
, 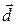 .
.
Следствие 3.4.4. Каковы бы ни были три некомпланарных вектора линейного пространства V 3, любой четвертый вектор из этого пространства может быть разложен по этим векторам.
 2015-01-21
2015-01-21 3771
3771