Методические указания. Данный метод является одним из методов повышенной точности

Данный метод является одним из методов повышенной точности. Пусть на отрезке [0,b] требуется найти решение уравнения

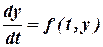(1)

с начальным условием 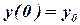. Разобьем отрезок [0,b] на n равных частей точками 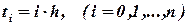, где 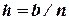- шаг интегрирования. Каждое последующее значение функции 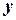определяется через предыдущее

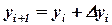. (2)

При этом для нахождения приращения 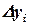вычисляются четыре коэффициента

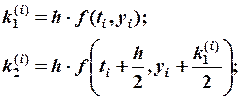
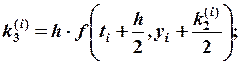(3)

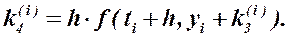
Затем определяется 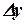по формуле

(4)

и подставляется в выражение (2). Вычисление начинается с 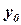и заканчивается 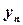. Таким образом на каждом шаге необходимо вычислить четыре значения функции 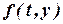, входящих в коэффициенты уравнений (3) сомножителями к шагу интегрирования 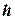. Геометрическая интерпретация коэффициентов 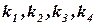следующая. Пусть кривая М₀СМ₁ (рис.1) есть решение дифференциального уравнения (1). Точка С этой кривой лежит на прямой, параллельной оси y и делящей отрезок 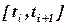пополам, B и G – точки пересечения касательной, проведенной к кривой в точке М₀, с ординатами АС и N₁M₁. Тогда число 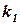с точностью до множителя 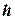есть угловой коэффициент касательной кривой М₀СМ₁, то есть

.

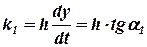Точка B имеет координаты 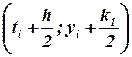. Следовательно 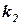с точностью до множителя 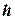есть угловой коэффициент касательной проведенной в точке В (BF-отрезок касательной)

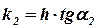
Через точку М₀ проведем прямую, параллельную отрезку BF, тогда точка D имеет координаты 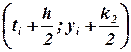и 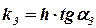есть угловой коэффициент касательной проведенной к интегральной кривой в точке D. DR₁ – отрезок этой касательной.

.

Рис. 1 Геометрическая интерпретация коэффициентов k_i

Через точку M₀ проведем прямую, параллельную DR₁ , которая пересечет вертикаль в конце шага в точке 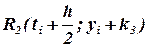. Тогда 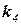с точностью до множителя 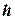определяет угловой коэффициент касательной, проведенной к интегральной кривой в точке , .

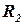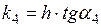Таким образом, расчетное значение 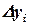связано с углами 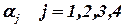соотношением:

.

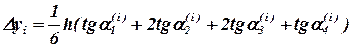Предварительная оценка погрешности делается после двойного просчета по формуле:

;

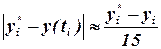где 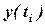- значение точного решения, 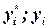- приближенные значения, полученные с шагом 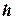и 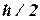соответственно. Если 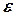- заданная точность, то шаг выбирают так, чтобы выполнялось условие: .

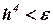Метод может быть применен к решению уравнений более высокого порядка путем сведения к системе дифференциальных уравнений первого порядка. Также возможно решение системы дифференциальных уравнений