По определению веса разряда
pi = si,
где i — номер разряда, а s — основание системы счисления.
Тогда, обозначив цифры числа как ai, любое число, записанное в позиционной системе счисления, можем представить в виде:
x = ansn + an-1sn-1 +... + a2s2 + a1s1 + a0s0 + a-1s-1 +...
Например, для системы счисления с основанием 4:
1302.24 = 1⋅43 + 3⋅42 + 0⋅41 + 2⋅40 + 2⋅4-1
Выполнив вычисления, мы получим значение исходного числа, записанное в десятичной системе счисления (точнее, в той, в которой производим вычисления). В данном случае:
1302.24 = 1⋅43 + 3⋅42 + 0⋅41 + 2⋅40 + 2⋅4-1 =
= 1⋅64 + 3⋅16 + 0⋅4 + 2⋅1 + 2⋅0,25 =
= 64 + 48 + 2 + 0,5 = 114,5
Таким образом, для перевода числа из любой системы счисления в десятичную следует:
- пронумеровать разряды исходного числа;
- записать сумму, слагаемые которой получаются как произведения очередной цифры на основание системы счисления, возведенное в степень, равную номеру разряда;
- выполнить вычисления и записать полученный результат (указав основание новой системы счисления — 10).
Примеры:
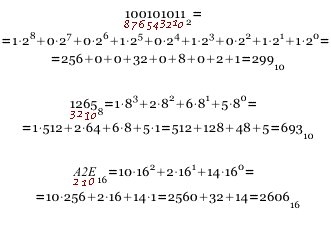
 2015-01-21
2015-01-21 490
490








