Система уравнений описывающих процессы электромеханического преобразования энергии
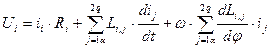
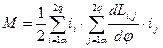
 нелинейна, т.к. содержит произведения переменных (wi×ij) и (ii×ij), а также переменные коэффициенты собственных и взаимных индуктивностей. Поэтому она неудобна для практического использования. Ее можно преобразовать путем замены действительных переменных фиктивными переменными при условии сохранения одинаковости математического описания и сохранения неизменной мощности.
нелинейна, т.к. содержит произведения переменных (wi×ij) и (ii×ij), а также переменные коэффициенты собственных и взаимных индуктивностей. Поэтому она неудобна для практического использования. Ее можно преобразовать путем замены действительных переменных фиктивными переменными при условии сохранения одинаковости математического описания и сохранения неизменной мощности.
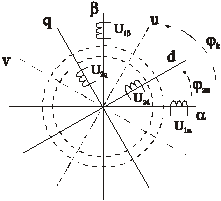
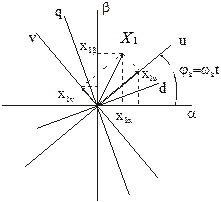
Коэффициенты самоиндукции и взаимоиндукции зависят от угла поворота ротора машин, т.е. от углового взаимного положения обмоток статора и ротора. Чтобы они были постоянными и не зависели от угла поворота осей ротора d,q относительно осей a,b статора, желательно, чтобы обмотки обобщенной машины 1a и 2d, а также 1bи 2q были неподвижны относительно друг друга. Для этого изобразим еще оси u,v на схеме обобщенной машины, которые вращаются в пространстве с угловой скоростью wк.
На этих осях располагаем расчетные обмотки (физически этих обмоток нет) статора и ротора. Считаем что эти обмотки создают такие же МДС, что и реальные обмотки. Коэффициенты самоиндукции в этом случае будут постоянными, т.к. обмотки неподвижны друг относительно друга.
|
|
|
Сделаем преобразования реальных переменных, соответствующих обмоткам, расположенными на осях a,b,d,q к фиктивным переменным, соответствующим расположению обмоток на осях u,v: Преобразования делаем только для обмоток статора, ибо для обмоток ротора преобразования аналогичны.
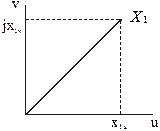
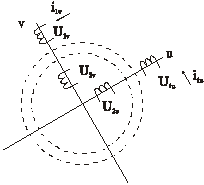 Представляем каждую реальную переменную (i,u,y) в виде вектора Х, являющимся геометрической суммой мгновенных векторов этой переменной. Пусть некоторая переменная в виде вектора Х, соответствует току, или напряжению, или потокосцеплению статора. Проекции этой реальной переменной на оси a,b,d,q равны Х1a, Х1b, Х2d, Х2q. Соответствующие им новые переменные в системе координат u,n определяется как суммы проекций реальных переменных на оси u,v. Например, составляющие вектора Х1u определяются как проекции векторов Х1a и Х1b на ось u, а составляющие вектора Х1v- как проекции этих же векторов на ось V. Просуммировав проекции по осям, получим формулы прямого преобразования для статорных переменных (см. рис.).
Представляем каждую реальную переменную (i,u,y) в виде вектора Х, являющимся геометрической суммой мгновенных векторов этой переменной. Пусть некоторая переменная в виде вектора Х, соответствует току, или напряжению, или потокосцеплению статора. Проекции этой реальной переменной на оси a,b,d,q равны Х1a, Х1b, Х2d, Х2q. Соответствующие им новые переменные в системе координат u,n определяется как суммы проекций реальных переменных на оси u,v. Например, составляющие вектора Х1u определяются как проекции векторов Х1a и Х1b на ось u, а составляющие вектора Х1v- как проекции этих же векторов на ось V. Просуммировав проекции по осям, получим формулы прямого преобразования для статорных переменных (см. рис.).
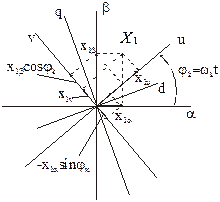
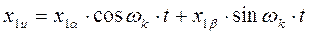
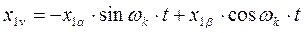
Аналогично формулы прямого преобразования для роторных переменных имеют вид (с учетом угла jэл).
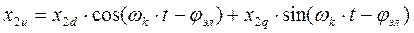
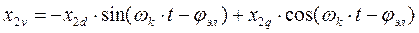
Как реальные переменные Х1a, Х1b, так и преобразованные Х1u и Х1v, являются проекциями на соответствующие оси одного и того же результирующего (обобщенного) вектора Х.
Переход от преобразованных, т.е. фиктивных переменных к реальным переменным обобщенной машины осуществляется с помощью формул обратного преобразования, которые можно получить с помощью аналогичных построений (см. рис.).
|
|
|
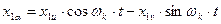
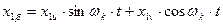
Аналогично для роторных переменных с учетом угла поворота ротора jэл.
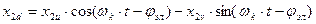
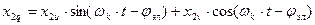 .
.
Пользуясь полученными формулами, преобразуем уравнения электрического равновесия и уравнения потокосцеплений к осям u,v. Для получения преобразованных уравнений в уравнениях электрического равновесия и уравнениях потокосцеплений с помощью формул преобразований заменим все реальные переменные, выразив их в осях u,v. Для пояснения сущности ограничимся только преобразованием уравнений равновесия для цепи статора, т.к. для ротора преобразования будут аналогичными. С этой целью подставляем выражения реальных переменных в уравнения обратного преобразования:
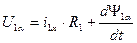
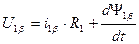
В результате получим:
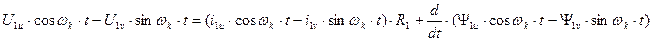
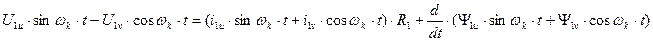
Продифференцировав произведения Y на тригонометрические функции угловой координаты, умножим 1-е из полученных уравнений на 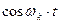 , а 2-е – на
, а 2-е – на 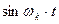 и складываем полученные уравнения. После приведения подобных членов получим уравнение равновесия для оси U. Умножая, затем 1-е из ранее полученных уравнений на -
и складываем полученные уравнения. После приведения подобных членов получим уравнение равновесия для оси U. Умножая, затем 1-е из ранее полученных уравнений на - 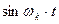 , а 2-е – на
, а 2-е – на 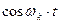 и выполнив аналогичные операции, что и в первом случае, получим уравнение электрического равновесия для оси V.
и выполнив аналогичные операции, что и в первом случае, получим уравнение электрического равновесия для оси V.
Аналогично можно получить преобразованные уравнения электрического равновесия для цепи ротора. В результате система уравнений электромеханической характеристики обобщенной машины будет иметь вид:
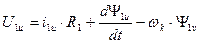
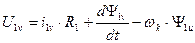
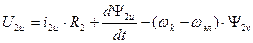
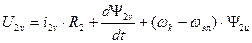 ,
,
где 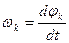 ;
; 
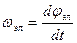 , а 3-ие слагаемые в правых частях уравнений – это ЭДС вращения.
, а 3-ие слагаемые в правых частях уравнений – это ЭДС вращения.
Аналогично можно получить преобразованные уравнения потокосцеплений: Но проще их можно написать исходя из физического смысла и пользуясь следующей схемой обобщенной машины.
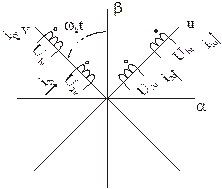 Потокосцепление каждой обмотки определяется собственной индуктивностью L1 или L2 и взаимной индуктивностью L12 с другой обмоткой, расположенной на той же оси. Взаимодействие с токами других обмоток отсутствует, т.к. их оси сдвинуты на jэл=90°, т.о.
Потокосцепление каждой обмотки определяется собственной индуктивностью L1 или L2 и взаимной индуктивностью L12 с другой обмоткой, расположенной на той же оси. Взаимодействие с токами других обмоток отсутствует, т.к. их оси сдвинуты на jэл=90°, т.о.
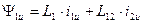
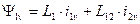
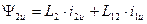
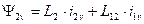
Если в выражении электромагнитного моменты неявнополюсной машины реальные токи
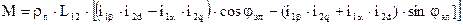
заменить на преобразованные по формулам обратного преобразования, получим после преобразований: 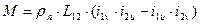 .
.
Если выразить токи через потокосцепления статора y1 или ротора y2 или и статора y1 и ротора y2, можно получить следующие выражения электромагнитного момента обобщенной машины:
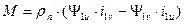
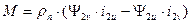
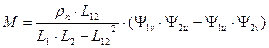
Объединив уравнения электромеханической характеристики с уравнением электромагнитного момента, получим математическое описание динамической механической характеристики обобщенной машины:
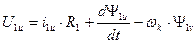
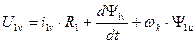
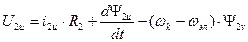
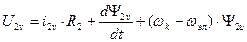
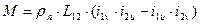
Преобразованную систему уравнений динамической механической характеристики можно представить в комплексной (векторной) форме, если ось U принять за действительную, а ось V – за мнимую.
 Напряжения, токи, потокосцепления в выше написанных уравнениях являются проекциями результирующих (обобщенных) векторов этих величин на оси U и V,
Напряжения, токи, потокосцепления в выше написанных уравнениях являются проекциями результирующих (обобщенных) векторов этих величин на оси U и V,
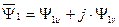
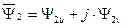
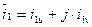
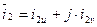
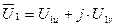
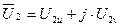
Теперь уравнения динамической механической характеристики будут иметь вид:
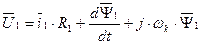
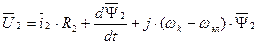
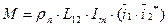 , где
, где
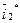 - величина, комплексно сопряженная величине
- величина, комплексно сопряженная величине 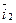 .
.
Символ Im(imaginary) означает, что в скобках стоит произведение мнимых частей комплексных токов i1 и i2*.
Выбор скорости wк координатных осей U,V.
Возможны следующие варианты выбора wк:
1. Выбор wк=0. Обеспечивает преобразование реальных переменных ротора, выраженных в осях d,q, к неподвижным осям a,b, жестко связанным со статором. Оси u,v в этом случае совпадают (совмещены) с осями a,b. Уравнения динамической механической характеристики для этого случая:
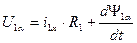
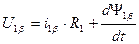
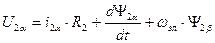
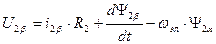
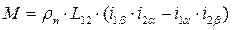
Эти уравнения используют в тех случаях, когда желательно оперировать действительными переменными статора. Преобразованные напряжения и токи обмоток машины остаются переменными и имеют частоту, равную частоте тока статора. ЭДС вращения в статоре не наводится, т.к. обмотки, расположенные на осях u,v, неподвижны относительно статора.
|
|
|
2. Выбор wк=wэл. Соответствует преобразованию реальных переменных машины к осям d,q, жестко связанным с ротором машины. Оси u,v в этом случае совмешены с осями d,q. Уравнения для обмоток статора будут преобразовываться, а уравнения для обмоток ротора – нет, т.к. ротор связан с осями d,q следовательно, с осями u,v жестко. Уравнения в осях d,q принимают вид:
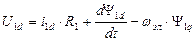
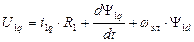
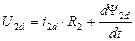
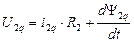
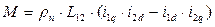
В роторе ЭДС вращения не наводится, поскольку относительно осей u,v ротор неподвижен.
Напряжения и токи здесь также как и при wк=0 являются переменными, но как в роторе, так и в статоре имеют частоту ротора, т.е. 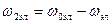 .
.
Эти уравнения целесообразно использовать для анализа процессов в синхронных машинах, когда в роторе протекает постоянный ток.(ток возбуждения). В синхронных машинах в установившимся режиме 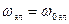 и
и 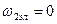 .
.
3. Выбор 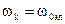 . Соответствует преобразованию реальных переменных к осям x,y, вращающимся синхронно со скоростью поля машины, т.е. неподвижных относительно поля статора.
. Соответствует преобразованию реальных переменных к осям x,y, вращающимся синхронно со скоростью поля машины, т.е. неподвижных относительно поля статора.
Естественно, что поскольку обмотки статора и ротора, связанные с осями u,v, неподвижны относительно друг друга, но вращаются вместе с этими осями со скоростью поля, то частота токов в них равна 0, т.е. они являются постоянными.
Уравнения динамической механической характеристики обобщенной машины в осях x,y.
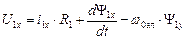
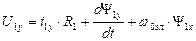
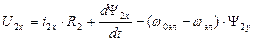
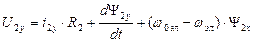
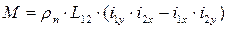
В осях x,y реальные переменные напряжения, приложенные к статору преобразуются в постоянное напряжение U1макс=const, приложенное только к обмотке, расположенной на оси х.
Действительно, пусть к реальным обмоткам статора приложена симметричная система напряжений 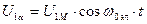
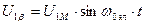 .
.
Если с помощью формул прямого преобразования преобразовать U1a и U1b в соответствующие им напряжения U1x и U1y и учесть, что wк=wэл, получим:
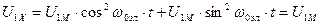
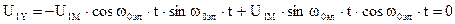
 2015-01-21
2015-01-21 1509
1509
