Указания к выполнению работы

Проверка достаточных условий сходимости итерационной последовательности может проводиться различными способами. Один из них состоит в проверке доминирования по модулю элементов на главной диагонали для матрицы коэффициентов при неизвестных, составленной для исходной СЛУ. Если такие условия не выполняются, то следует преобразовать исходную СЛУ с помощью линейных операций.

После преобразования СЛУ для удовлетворения достаточных условий сходимости и перед применением итерационных методов необходимо еще раз преобразовать СЛУ так, чтобы в левой части каждого уравнения оставались переменные с номером соответствующего уравнения. Для СЛУ система должна принять вид: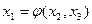

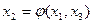
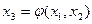
В качестве начального приближения может быть выбран вектор свободных членов.

Расчеты проводить в следующей таблице.

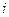
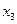
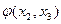
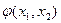
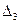
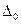
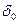
Условие остановки по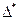

Здесь 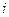– номер итерации; значения , , 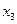- текущие решения СЛУ; 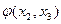, , 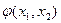- правые части первого, второго и третьего преобразованный уравнений; , , 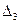- текущие оценки абсолютной погрешности для , , 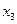; 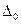= max(, , 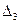) – это оценка абсолютной погрешности всей СЛУ на текущей итерации; 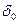= 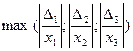- относительная погрешность решения всей СЛУ (используется для построения графика). Условие остановки состоит в анализе 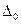< 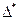. Это условие будет выполнено, если существует покомпонентная сходимость, т.е. наблюдается уменьшение погрешности для каждой переменной с ростом числа итераций.

Кривые изменения оценок абсолютных погрешностей для каждой переменной и в целом для СЛУ в зависимости от числа итераций должны располагаться на одном графике, а кривая относительной погрешности – на другом графике.