Используемые уравнения. Принята концепция изотропной турбулентной вязкости. Основанная на приближении Буссинеска. Напряжения Рейнольдса считаются пропорциональными осреднённым по времени скоростям деформаций. Введением коэффициента турбулентной вязкости 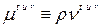 , данная концепция выражается как
, данная концепция выражается как
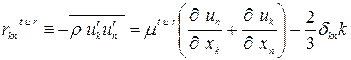 (9)
(9)
Коэффициент эффективной вязкости вычисляется как сумма молекулярного и турбулентного коэффициентов
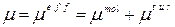
В данной работе для определения коэффициента турбулентной вязкости используется двухпараметрическая высокорейнольдсовая 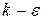 модель турбулентности со следующими уравнениями и замыкающими соотношениями
модель турбулентности со следующими уравнениями и замыкающими соотношениями 
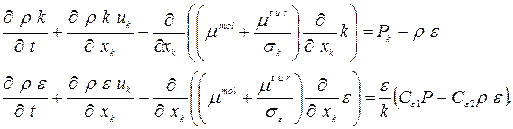 (10)
(10)
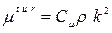 /
/ 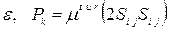 (11)
(11)
Где 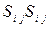 - квадрат осреднённого тензора напряжений. Константами модели являются
- квадрат осреднённого тензора напряжений. Константами модели являются
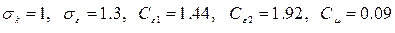 (12)
(12)
Как показали Като и Лаундер, 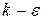 модель в стандартной формулировке переоценивает величину генерации кинетической энергии турбулентности в областях с малыми скоростями сдвиговых деформаций. Для устранения этого эффекта Като и Лаундер переопределили генерационный член через произведение вращательного и деформационного сомножителей
модель в стандартной формулировке переоценивает величину генерации кинетической энергии турбулентности в областях с малыми скоростями сдвиговых деформаций. Для устранения этого эффекта Като и Лаундер переопределили генерационный член через произведение вращательного и деформационного сомножителей
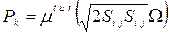 , (13)
, (13)
Где 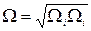 - модуль осреднённой завихрённости.
- модуль осреднённой завихрённости.
В конечном счёте, к разработке очень большого числа моделей подобного рода.
Фундаментальную роль в теории турбулентности, основанной на использовании уравнений для вторых моментов, сыграли работы А.Н. Колмогорова (1942) 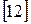 и Прандтля – Вигхарда (1945)
и Прандтля – Вигхарда (1945) 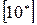 , в которых была предложена гипотеза, связывающая коэффициент турбулентной вязкости
, в которых была предложена гипотеза, связывающая коэффициент турбулентной вязкости 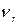 и кинетическую энергию турбулентности
и кинетическую энергию турбулентности 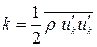
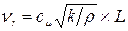 (16)
(16)
Здесь 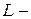 интегральный масштаб турбулентности,
интегральный масштаб турбулентности, 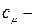 эмпирическая постоянная.
эмпирическая постоянная.
В предложении о градиентном механизме турбулентной диффузии, принятом в работе А.Н. Колмогорова, уравнение для 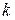 приобретает вид
приобретает вид
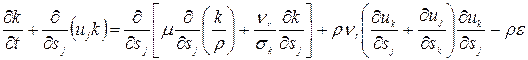 (17)
(17)
Здесь 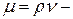 коэффициент динамической вязкости;
коэффициент динамической вязкости; 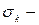 эмпирическая постоянная.
эмпирическая постоянная.
Скорость диссипации энергии турбулентности 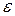 в соответствии с гипотезой Колмогорова – Прандтля выражается при больших числах Рейнольдса через кинетическую энергию
в соответствии с гипотезой Колмогорова – Прандтля выражается при больших числах Рейнольдса через кинетическую энергию 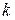 и интегральный масштаб
и интегральный масштаб 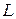 соотношением
соотношением
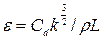 , (18) где
, (18) где 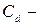 эмпирическая постоянная.
эмпирическая постоянная.
Принятие гипотезы (18) означает, что процессом, определяющим скорость диссипации, является не сам процесс собственно диссипации, т.е. процесс превращения кинетической энергии «мелкомасштабных вихрей» в тепло, а процесс переноса энергии последовательно от «больших вихрей» к «меньшим». Этот каскадный процесс, как предполагается, зависит лишь от величин 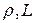 и
и 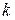 и не зависит от вязкости.
и не зависит от вязкости.
Если исключить из формулы Колмогорова – Прандтля (16) интегральный масштаб 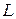
 с помощью равенства (18), то получится соотношение, связывающее коэффициент турбулентной вязкости
с помощью равенства (18), то получится соотношение, связывающее коэффициент турбулентной вязкости 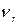 , кинетическую энергию турбулентности
, кинетическую энергию турбулентности 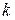 и скорость диссипации энергии
и скорость диссипации энергии 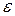 .
.
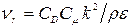 (19)
(19)
Для использования уравнений (17) – (18) необходимо задание интегрального масштаба турбулентности. В наиболее простых моделях для определения этого масштаба использовалось допущение о его адекватности пути смешения, определяемого по формулам типа формулы Прандтля (15). В более сложных моделях вместо «алгебраических» выражений для масштаба турбулентности использовались дифференциальные уравнения. Однако наибольшее распространение получили двухпараметрические модели, в которых вместо уравнения для масштаба турбулентности используется уравнение для скорости диссипации энергии турбулентности 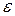 . Семейство этих моделей получило наименование
. Семейство этих моделей получило наименование 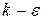 моделей турбулентности.
моделей турбулентности.
Использование в качестве второго параметра скорости диссипации 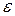 вместо масштаба турбулентности
вместо масштаба турбулентности 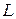 , с которым эта величина связана соотношением (18), даёт ряд практических преимуществ.
, с которым эта величина связана соотношением (18), даёт ряд практических преимуществ.
Уравнение для 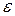 можно строго получить из уравнений Навье - Стокса путём соответствующей процедуры, включающей осреднение по Рейнольдсу. Это уравнение оказывается незамкнутым. Для замыкания необходимы модельные представления отдельных его членов. Ограничимся приведением следующей формы этого уравнения
можно строго получить из уравнений Навье - Стокса путём соответствующей процедуры, включающей осреднение по Рейнольдсу. Это уравнение оказывается незамкнутым. Для замыкания необходимы модельные представления отдельных его членов. Ограничимся приведением следующей формы этого уравнения
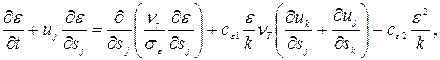 (20)
(20)
Играющего базисную роль для многочисленного семейства 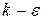 моделей. Приведём стандартные значения эмпирических постоянных, входящих в это уравнение:
моделей. Приведём стандартные значения эмпирических постоянных, входящих в это уравнение: 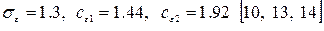 .
.
Уравнение (20) может быть использовано совместно с уравнениями(17),

ЛЕКЦИЯ № 1. Введение
 2014-09-04
2014-09-04 418
418







