Язык логики предикатов

Алфавит:

а) р, q, r, s, p 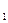,... — пропозициональные переменные;

б) а, b, с, d, a 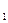, b 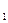... — индивидные константы;

в) х, у, z, х 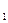, y 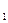,... — индивидные переменные;

г) P 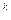, Q^k, R^k, S^k, P 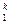, Q 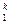,... — k-местные предикаторные символы (k = 1, 2, 3,...);

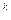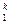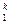д) f , q ^k, f , q , f 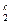, … - k-местные предметные функторы (символы для знаков k-местных предметных функций);

е) 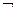, , 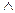, , 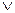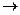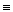— логические термины;

ж) 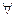, 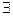— логические термины, называемые соответственно квантором общности и квантором существования. Читаются «все» («каждый»), «существует» («некоторые»);

з) (,) — скобки;

и), — запятая.

Выражения языка логика предикатов называются формулами. Среди формул выделяют правильно построенные (ППФ).

Определению правильно построенной формулы предшествует определение терма:

а) индивидные константы и индивидные переменные являются термами;

б) если t 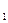..., t_k — термы, а F 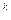— знак k- местной предметной функции, F^k (t 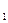,..., t_k) — терм;

в) ничто иное не является термом.

Определение ППФ:

а) пропозициональный символ является ППФ;

б) если t 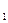..., t_k — термы, а А 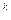— k- местный предикатор, то A^k (t 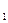_;..., t 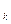) - ППФ;

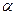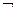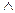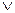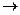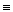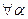в) если А и В — ППФ, а — индивидная переменная, то А, (В С), (В С), (A В), (А В), A, 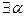А - ППФ;

г) ничто иное не является ППФ.