Разрешенные КВ должны быть ортогональны векторам контрольной матрицы. Исходя из этого, найдем условия, которым должны удовлетворять КВ кода, построенного по контрольной матрице (2.16):
| 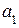
| 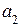
| 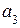
| 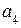
| 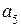
| 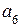
| 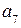
| – 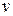
| ||||||
– 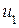
| ||||||||||||||
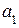
| 
| 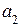
| 
| 
| 
| 
| 
| 
| 
| = 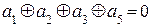
|
| 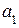
| 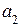
| 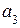
| 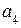
| 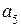
| 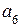
| 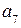
| – 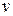
| ||||||
– 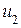
| ||||||||||||||

| 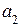
| 
| 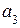
| 
| 
| 
| 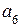
| 
| 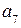
| = 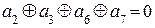
|
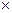
| 
| 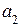
| 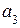
| 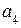
| 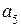
| 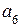
| 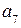
| – 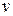
| ||||||
– 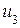
| ||||||||||||||

| 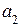
| 
| 
| 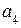
| 
| 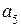
| 
| 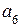
| 
| = 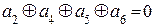
|
Итак, любой формируемый КВ должен удовлетворять условиям:
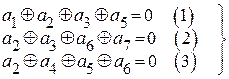 (2.17)
(2.17)
Для любой информационной части равенства (2.17) достигаются путем подбора контрольных разрядов, в качестве которых выбираются разряды, встречающиеся только в одной проверке. Таковыми являются 1, 4 и 7 разряды (соответствуют столбцам контрольной матрицы 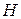 , содержащим только одну 1). Разряд
, содержащим только одну 1). Разряд 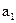 обеспечивает ортогональность с вектором
обеспечивает ортогональность с вектором 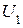 ;
; 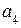 – с
– с 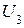 ;
; 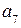 – с
– с 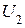 .
.
Из системы проверочных равенств (2.17) определяем, какими должны быть проверочные символы при формировании конкретной комбинации безизбыточного кода:
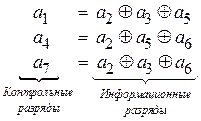
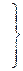 (2.18)
(2.18)
Пример
Закодировать число 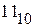 линейным кодом, использующим контрольную матрицу (2.16).
линейным кодом, использующим контрольную матрицу (2.16).
Решение
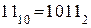 .
.
Начиная со старших разрядов, располагаем полученную безизбыточную двоичную комбинацию на отведенные ей позиции (2, 3, 5 и 6 разряды).
| Контрольные разряды | |||||||||||
| |||||||||||
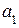
| 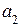
| 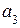
| 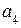
| 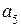
| 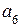
| 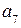
| |||||
Подставляя значения информационных символов в уравнения (2.18), находим значения проверочных символов:
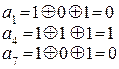
Подставив полученные значения контрольных разрядов на отведенные позиции, получаем:
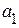
| 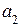
| 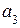
| 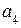
| 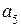
| 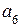
| 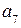
|
 2015-01-21
2015-01-21 572
572








