| Вари-ант | Уравнение связи | A

| b 
| c |
Q=a2b+1/c 
| 11,55 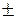 0,05 0,05 
| 10,00 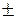 0,05 0,05
| 12,7 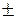 0,1 0,1 
| |
| Q=15a3+b2/c2 | 8,05  0,05 0,05
| 10,00  0,03 0,03
| 12,0  0,1 0,1
| |
Q=0,5a+ 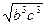
| 12,0  0,1 0,1
| 1,23  0,01 0,01
| 1,003  0,001 0,001
| |
Q=a2/0,5-b 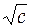
| 13,05  0,05 0,05
| 13,08  0,01 0,01
| 12,1  0,1 0,1
| |
Q=a3/2+ 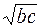
| 81  1 1
| 124,1  0,1 0,1
| 10,05  0,05 0,05
| |
Q=32 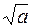 +1/b3c3 +1/b3c3
| 135  1 1
| 1,208  0,001 0,001
| 1,25  0,01 0,01
| |
| Q=1,5a3+b2c3 | 1,81  0,01 0,01
| 1,3205  0,0005 0,0005
| 1,241  0,001 0,001
| |
| Q=81(а3/b3)-c0,5 | 4,4  0,1 0,1
| 6,83  0,01 0,01
| 22,08  0,01 0,01
| |
Q=1,1 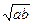 +c3 +c3
| 12,05  0,05 0,05
| 6,8  0,1 0,1
| 1,478  0,001 0,001
| |
| Q=a3-b2c4/168 | 2,03  0,01 0,01
| 1,46  0,01 0,01
| 0,705  0,005 0,005
|
Задача 3. Определить 10 значений членов арифметической прогрессии с известным значением первого члена и разности прогрессии, а также 10 значений ряда предпочтительных чисел. Построить графики.
Таблица 3
 2015-02-24
2015-02-24 288
288








