Т.к. ток окружен магнитным полем, встает вопрос, где локализована собств. этого поля. Ответ на этот вопрос был дан опытным путем при исследовании переменных магнитных полей (эл/магн. волн).
Т.к. ЭМВ заключают в себе и переносят определенную энергию, то энергия сосредоточена в самом поле.
Рассмотрим идеальный соленоид.
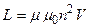
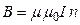
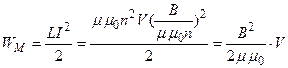
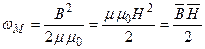 - объемная плотность энергии магн. поля
- объемная плотность энергии магн. поля
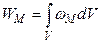 (*)
(*)
Замечание: для ферромагнетиков
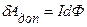
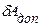 идет на создание магнитного поля и на приращение внутренней энергии среды (на нагревание).
идет на создание магнитного поля и на приращение внутренней энергии среды (на нагревание).
Покажем, что в случае справедливости формулы (*), формула для энергии магн. поля имеет вид:
Возьмем прямоугольный контур с током.
Окружим элемент трубки dS, ось которой совпадает c 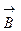
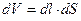
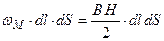
Энергия сосредоточена во всей трубке
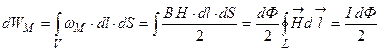
Просуммируем все элем. энергии всех трубок. Получим полную энергию магнитного поля
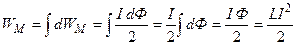
Замечание:
Т.к. 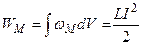 Þ
Þ
 Þ
Þ 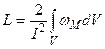 - эта формула позволяет найти индуктивность энергетическим способом и в некоторых случаях позволяет проще найти L, чем из определения.
- эта формула позволяет найти индуктивность энергетическим способом и в некоторых случаях позволяет проще найти L, чем из определения.
Ввиду того, что в некоторых случаях трудно вычислить магнитный поток, создаваемый контуром с током.
Рассмотрим пример:
Рассмотрим коаксиальный кабель и найдем индуктивность на единицу длины.
По теореме о циркуляции 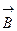 рассчитаем
рассчитаем 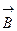 этого кабеля
этого кабеля
1) r £ a
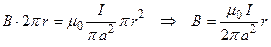
2) a £ r £ b
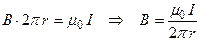
3) B = 0
а) r  a
a
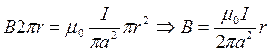
б) 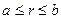
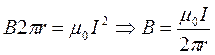
в) r>b

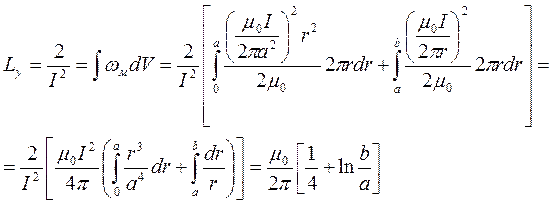
При включении источников 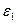 и
и 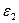 в контурах возбуждается
в контурах возбуждается  и
и 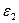 в контурах возбуждается
в контурах возбуждается  и
и 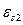 при этом магнитный поток изменится
при этом магнитный поток изменится
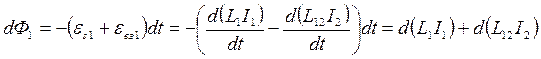
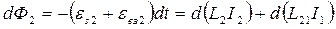
Дополнительная работа сторонних сил источника  совершается против
совершается против  и
и 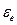 образующихся при включении источников в первом и втором контуре.
образующихся при включении источников в первом и втором контуре.
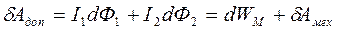 - и эта дополнительная работа идёт на приращение энергии магнитного поля этих контуров
- и эта дополнительная работа идёт на приращение энергии магнитного поля этих контуров
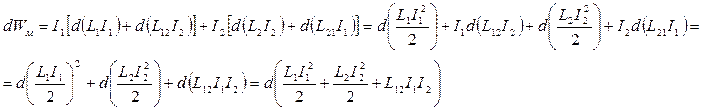
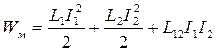 (*)
(*)
Энергия магнитного поля двух контуров с токами.
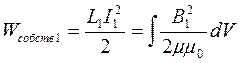 - собственная энергия тока
- собственная энергия тока 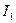
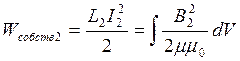 - собственная энергия тока
- собственная энергия тока 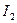
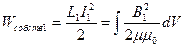 - энергия взаимодействия токов (**)
- энергия взаимодействия токов (**)
Получим формулу (*) непосредственно.
В некоторой точке пространства находится контур с током 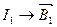 , а контур с током
, а контур с током 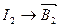 .
.
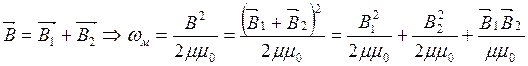
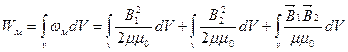
аналогично.
Выводы:
1) из формул для собственной энергии магнитного поля видно, что собственные энергии магнитного поля величины строго положительны
2) энергии магнитного поля двух контуров с током не является величиной адиативной
3) взаимная энергия магнитного поля двух контуров с током может быть величиной как положительной, так и отрицательной
4) из формулы (**) можно получить ещё один метод расчета взаимной индуктивности без контуров ферромагнетиков
 2015-02-24
2015-02-24 2407
2407
