Тема. Указатели на функции.
Требования и общие указания к заданиям.
· Составить функцию, которая по заданной формуле (Симпсона, трапеций, прямоугольников и др.) вычисляет значение определённого интеграла от произвольной функции одной переменной или решает произвольное нелинейное уравнение f(x)=0 с помощью заданного численного метода.
· В качестве одного из параметров этой функции должен быть указатель на подынтегральную функцию или указатель на функцию левой части уравнения f(x)=0.
· Функцию для вычисления определённого интеграла проверить, используя аналитическое выражение для первообразной или с помощью какой-нибудь системы компьютерной математики (Mathcad, Mathematica и др.).
· При решении нелинейных уравнений корни отделить графически или другим способом. Отрезок, на котором находится корень, для функции предполагается известным.
· Запрограммировать проверку найденных решений нелинейных уравнений.
Варианты заданий.
В. Задачи второго среднего уровня.
1.Составить функцию, которая вычисляет значение определённого интеграла 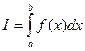 от произвольной функции одной переменной по формуле правых прямоугольников:
от произвольной функции одной переменной по формуле правых прямоугольников:
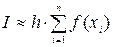 ,
,
где n фиксировано, 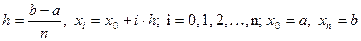 . Составленную функцию проверить для вычисления интеграла
. Составленную функцию проверить для вычисления интеграла 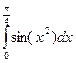 . Значение функции y=sin(t) вычислять с заданной точностью e., используя разложение в ряд Тейлора:
. Значение функции y=sin(t) вычислять с заданной точностью e., используя разложение в ряд Тейлора: 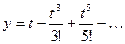
2. Составить функцию, которая вычисляет значение определённого интеграла 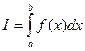 от произвольной функции одной переменной. по формуле левых прямоугольников
от произвольной функции одной переменной. по формуле левых прямоугольников
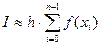 ,
,
где n фиксировано, 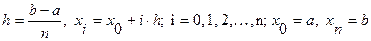 . Составленную функцию проверить для вычисления интеграла
. Составленную функцию проверить для вычисления интеграла 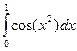 . Значение функции y=cos(t) вычислять с заданной точностью e., используя разложение в ряд Тейлора:
. Значение функции y=cos(t) вычислять с заданной точностью e., используя разложение в ряд Тейлора:
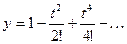
.
3. Составить функцию, которая вычисляет значение определённого интеграла 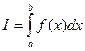 от произвольной функции одной переменной по формуле средних прямоугольников
от произвольной функции одной переменной по формуле средних прямоугольников
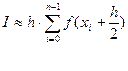 ,
,
где n фиксировано, 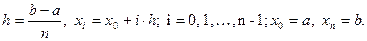 Составленную функцию проверить для вычисления интеграла
Составленную функцию проверить для вычисления интеграла 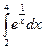 Значение функции y= et, где
Значение функции y= et, где
t= 1/x, вычислять с заданной точностью e, используя разложение в ряд Тейлора:
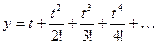
4. Составить функцию, которая вычисляет значение определённого интеграла 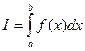 от произвольной функции одной переменной с помощью составной формулы трапеций:
от произвольной функции одной переменной с помощью составной формулы трапеций:
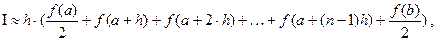
где n фиксировано, 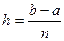 . С помощью составленной функции вычислить значение интеграла
. С помощью составленной функции вычислить значение интеграла 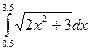 для n=3, 6, 9. Для вычисления y =
для n=3, 6, 9. Для вычисления y = 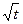 , где t=
, где t= 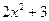 , составить и использовать функцию, которая реализует следующий итерационный алгоритм:
, составить и использовать функцию, которая реализует следующий итерационный алгоритм: 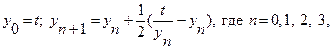 … Вычисления продолжаются до тех пор, пока не выполнится условие
… Вычисления продолжаются до тех пор, пока не выполнится условие 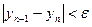 . Массив y не формируется, достаточно двух переменных для старого и нового значений y.
. Массив y не формируется, достаточно двух переменных для старого и нового значений y.
5. Составить функцию, которая вычисляет значение определённого интеграла 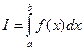 от произвольной функции одной переменной, используя составную формулу трапеций:
от произвольной функции одной переменной, используя составную формулу трапеций:
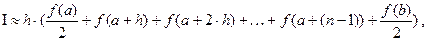
где n фиксировано, 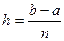 . С помощью составленной функции вычислить значения интеграла
. С помощью составленной функции вычислить значения интеграла 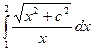 для с = 1, 1.2, 1.4, …, 2.8, 3. Для вычисления y =
для с = 1, 1.2, 1.4, …, 2.8, 3. Для вычисления y = 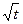 можно использовать стандартную встроенную функцию или вычислять по итерационной формуле, приведенной в варианте 4.
можно использовать стандартную встроенную функцию или вычислять по итерационной формуле, приведенной в варианте 4.
6. Составить функцию, которая вычисляет значение определённого интеграла 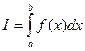 от произвольной функции одной переменной, используя составную формулу Симпсона:
от произвольной функции одной переменной, используя составную формулу Симпсона:
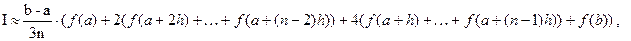
где n фиксировано, 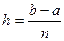 . С помощью составленной функции вычислить значение интеграла
. С помощью составленной функции вычислить значение интеграла 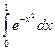 . Значение функции y= et, где t= -x2, вычислять с заданной точностью e, используя разложение в ряд Тейлора:
. Значение функции y= et, где t= -x2, вычислять с заданной точностью e, используя разложение в ряд Тейлора: 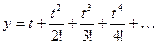
7. Составить функцию, которая вычисляет значение определённого интеграла 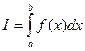 от произвольной функции одной переменной, используя составную формулу Симпсона:
от произвольной функции одной переменной, используя составную формулу Симпсона:
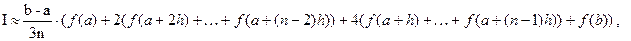
где n фиксировано, 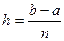 . С помощью составленной функции вычислить значение интеграла
. С помощью составленной функции вычислить значение интеграла 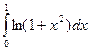 для n=6. Значение функции y= ln(1+t), где t=x2, вычислять с заданной точностью e, используя разложение в ряд Тейлора:
для n=6. Значение функции y= ln(1+t), где t=x2, вычислять с заданной точностью e, используя разложение в ряд Тейлора: 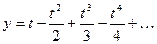 .
.
8. Составить функцию для вычисления определённого интеграла 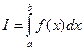 от произвольной функции одной переменной по следующей формуле:
от произвольной функции одной переменной по следующей формуле:
I 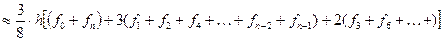 ,
,
где n фиксировано и кратно трём, 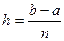 ,
, 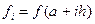 , С помощью составленной функции вычислить значения интегралов
, С помощью составленной функции вычислить значения интегралов 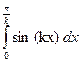 для k = 1/4, 1/2, 1, 2, 4.
для k = 1/4, 1/2, 1, 2, 4.
9.Составить функцию для приближённого решения произвольного нелинейного уравнения f(x)=0 методом деления отрезка пополам с точностью e. Используя эту функцию, решить уравнения 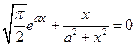 для a = 0.5+0.1k, k=0,1,2,3,4,5 с точностью e1=0.1.
для a = 0.5+0.1k, k=0,1,2,3,4,5 с точностью e1=0.1.
10. Составить функцию для приближённого решения произвольного нелинейного уравнения f(x)=0 методом простой итерации с точностью e. Используя эту функцию, решить уравнения 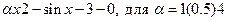 с точностью e1=0.0001. Указание. В методе простой итерации исходное уравнение приводится к виду x=j(x). Начиная с некоторого заданного начального значения
с точностью e1=0.0001. Указание. В методе простой итерации исходное уравнение приводится к виду x=j(x). Начиная с некоторого заданного начального значения 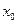 , строим последовательность по правилу
, строим последовательность по правилу 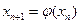 . Вычисления прекращаем, если на некотором шаге получим
. Вычисления прекращаем, если на некотором шаге получим 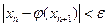 , где
, где 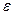 — заданная точность решения уравнения.
— заданная точность решения уравнения.
11. Составить функцию для приближённого решения произвольного нелинейного уравнения f(x)=0 методом Ньютона с точностью e. Используя эту функцию, решить уравнения 3x-ekx = 0 для k = 1, 2, 3, 4, 5 с точностью e1=10-5. Значение et вычислять с заданной точностью e2 = 10-6 с помощью разложения в ряд Тейлора
et = 1 + t + 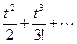 .
.
Указание. В методе Ньютона по заданному начальному приближению xо строим последовательность по правилу
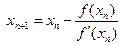 ; n=0,1, 2, 3, …
; n=0,1, 2, 3, …
Вычисления продолжаются до тех пор, пока не выполнится условие 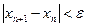 . Массив x не формируется, достаточно двух переменных для старого и нового значений x.
. Массив x не формируется, достаточно двух переменных для старого и нового значений x.
12. Составить функцию для приближённого решения нелинейного уравнения f(x)=0 с точностью e методом секущих. Используя эту функцию, решить уравнения 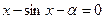 для
для 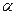 = 2(0.1)3 с точностью e1=10-5. Указание. В методе секущих по двум начальным приближениям
= 2(0.1)3 с точностью e1=10-5. Указание. В методе секущих по двум начальным приближениям 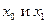 строим последовательность по правилу
строим последовательность по правилу
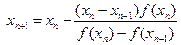 ; n= 1,2, 3, …
; n= 1,2, 3, …
Вычисления продолжаются до тех пор, пока не выполнится условие 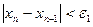 . Массив x не формируется, достаточно двух переменных для старого и нового значений x.
. Массив x не формируется, достаточно двух переменных для старого и нового значений x.
13. Составить функцию для решения произвольного нелинейного уравнения f(x) модифицированным методом секущих с точностью e. Используя эту функцию, решить уравнение 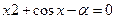 для
для 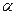 =3(0.5)7 с точностью e=
=3(0.5)7 с точностью e= 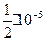 . Указание. В модифицированном методе секущих по двум начальным приближениям
. Указание. В модифицированном методе секущих по двум начальным приближениям 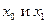 строим последовательность по правилу
строим последовательность по правилу
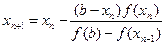 для n=1, 2, …,
для n=1, 2, …, 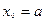 при
при 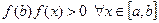 . Вычисления прекращаем, если на некотором шаге получим
. Вычисления прекращаем, если на некотором шаге получим 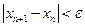 , где
, где 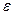 — заданная точность решения уравнения.
— заданная точность решения уравнения.
14. Составить функцию, которая находит приближенно, с точностью до 0,001, минимум произвольной функции от одной переменной на отрезке [ u, v ]. С помощью составленной функции найти минимум функции y= 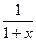 +sin(x) на отрезке (-0.9, 0.9). Значение функции y= sin (x) вычислять с заданной точностью e, используя разложение в ряд Тейлора:
+sin(x) на отрезке (-0.9, 0.9). Значение функции y= sin (x) вычислять с заданной точностью e, используя разложение в ряд Тейлора:
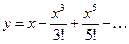
15. Составить функцию, которая выводит таблицу значений произвольной функции от одной переменной на отрезке [ u, v ] с шагом h. С помощью составленной функции построить таблицу значений функции y=arctg(x) на отрезке [ -1, 1 ] с шагом h=0.1. Значение функции y=arctg(x) вычислять с заданной точностью e, используя разложение в ряд: 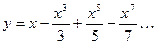
 2015-02-24
2015-02-24 624
624








