1. Вычислить для заданного натурального n:
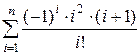 .
.
2.Найти n -й член числовой последовательности, которая определяется рекуррентной формулой
a 1 = 1, a 2 = 2, a 3 = 3, an +1 = 3 an + 2 an – + an –2.
3. Для заданных вещественном x и натуральном n найти значение полинома Чебышева Тn (x) по рекуррентной формуле:
T 0(x) = 1, T 1(x) = x, Tn +1(x) = 2 xTn (x) – Tn –1(x).
4. Найти значение функции С (m, n), где 0 < m < n, если:
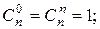
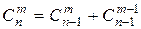 .
.
5. С помощью признака делимости на 3 проверьте, кратно ли данное натуральное число трём.
6. Найдите n -ю степень (n – натуральное число) числа а, используя рекурсивную функцию.
7. Найдите n -й член арифметической прогрессии с заданными первым членом а и разностью прогрессии d.
8. Найдите n -й член геометрической прогрессии с заданными первым членом b и знаменателем прогрессии q.
9. М етодом половинного деления уточните корень уравнения f (х) = 0.
10. Найти максимальный элемент массива а 1, а 2, …, аn.
11. В одномерном массиве найти i и j такие, что подпоследовательность аi, аi +1, …, аj является перевертышем.
12. В одномерном числовом массиве найдите подпоследовательность подряд идущих элементов, сумма которых максимальна.
13. Рассортировать одномерный массив методом простого выбора.
14. Запрограммировать алгоритм двоичного поиска элемента одномерного массива, равного данному числу.
15. Разработайте рекурсивную функцию нахождения значения функции Аккермана, которая определяется для всех неотрицательных целых аргументов m и n следующим образом:
А (0, n) = n + 1;
A (m, 0) = A (m – 1, 1), если (m > 0);
A (m, n) = A (m – 1, A (m, n – 1)), если (m, n > 0).
 2015-02-24
2015-02-24 1715
1715








