Матрицы переходов высшего порядка

Последовательность k дуг, которая в графе переходов ведет из одного состояния в другое, называется путем; k называется длиной пути. P^(k)_ij обозначает множество всех путей длины k, которые ведут из состояния σ_i в состояние σ_j. Множество P^(l)_ij, которое состоит из одной дуги, ведущей из σ_i в σ_j, будем обозначать π_ij. Если P^(l)_ij пусто (т. е. если ни одна дуга не ведет из σ_i в σ_j), то ему придается значение 0 (нуль).

Путь длины k, представляющий собой упорядоченную последовательность дуг πii₁, πi₁i₂,..., πi_k-1i₁ (рис. 2.9), символически изображается упорядоченным произведением

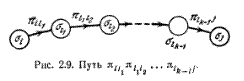
πii₁, πi₁i₂,..., πi_k-1i_1. Поскольку несуществующая дуга по определению соответствует нулевому сомножителю, то, если хотя бы одна дуга на пути, символически изображаемом вышеприведенным произведением, не существует, то все произведение становится равным нулю. Множество путей записывается как неупорядоченная сумма произведений; каждое произведение представляет элемент этого множества. Таким образом, где нулевые компоненты интерпретируются как несуществующие пути.

Лемма 2.2.

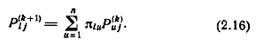
Доказательство. Применяя B.15), получим:

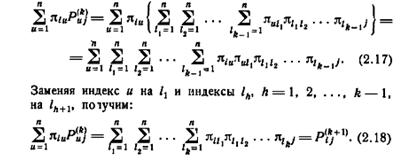
Для автоматов с n состояниями матрица переходов k-го порядка обозначается 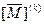и состоит из n строк n столбцов, обозначенных так же, как и в матрице [ M ]. Элемент (i, j) матрицы 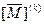обозначается e ^(k)_ij и определяется так:

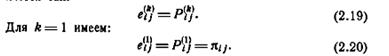
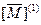записывается как 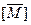и может быть, получена из [М] путем замены каждого ненулевого элемента (i, j) в матрице [М] на π_ij.

Умножение матриц переходов высшего порядка определяется следующим образом. Если 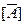имеет элемент (i, j), равный a _ij, 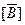— элемент (i, j), равный b _ij, и =

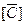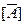
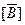= —элемент (i, j), равный c _ij, и если каждая из этих матриц является квадратной (n 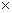n)-матрицей переходов высшего порядка, то

Умножение элементов a _iu и b _uj (каждый из них в общем случае представляет сумму произведений[15]) ассоциативно и дистрибутивно по отношению к сложению, но не коммутативно. Таким образом, умножение матриц переходов высших порядков аналогично умножению обычных матриц, за исключением того, что порядок сомножителей в каждом произведении a _iu b _uj должен быть сохранен, т. е. a _iu b _uj не эквивалентно b _uj a _iu.

Лемма 2.3.

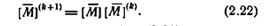
Доказательство. Из (2.19), (2.20) и (2.21) следует, что элемент (i, j) произведения матриц 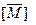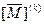является суммой 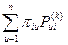. Однако, согласно (2.16) и (2.19), это — элемент 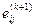, что доказывает лемму.

Теорема 2.3. Элемент (i, j) матрицы 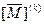, k = 1, 2,..., является множеством всех путей длины k, ведущих из состояния σ₁ в состояние σ _j в автомате М.

Доказательство. Теорема эквивалентна утверждению, что 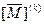= 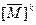. Для k=1 это равенство справедливо по построению. Если равенство справедливо для k = h, то из (2.22) получаем:

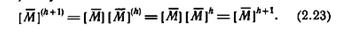
По индукции следует, что указанное равенство справедливо для любого k ≥ 1.

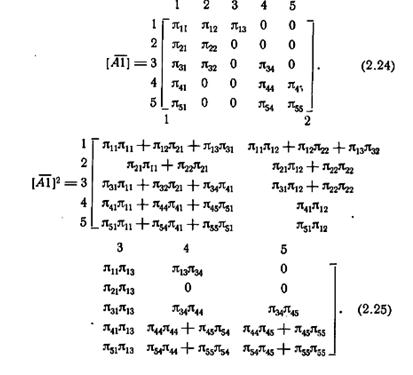
Теорема 2.3 показывает, что множество всех путей длины k, ведущих из одного состояния в другое, может быть построено систематически путем возведения матрицы 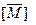в k -ю степень. Нижние индексы содержащихся в матрице путей соответствуют дугам, из которых составлены эти пути. Обращаясь к графу или матрице переходов, можно определить обозначения этих дуг, а следовательно, и соответствующие путям входные и выходные последовательности.

Например, (2.24) является матрицей переходов первого, а (2.25)—матрицей переходов второго порядка автомата А1, заданного матрицей переходов (2.12). Из (2.25) видно, в частности, что имеются два пути длиной 2 из состояния 3 в состояние 2, а именно π₃₁π₁₂ и π₃₂π₂₂ и нет пути длиной 2 из состояния 2 в состояние 4 или 5. Из (2.25) и (2.12) также можно заключить, что в состояние 2 можно попасть из состояния 5, если подавать входные последовательности ли, или πn, или πλ.